모두의 연구소 음성인식 풀잎스쿨에서 Introduction to Speech Processing(2E) 중 acousitc featrure extraction 부분 공부한 내용을 정리한 글입니다. 또한 한국 인공지능협회 오디오 처리 세션에서 공부한 내용도 함께 정리했음을 밝힙니다.
Index
오디오 데이터 전처리 (2) Fourier Transform & Spectrogram
오디오 데이터 전처리 (3) Cepstrum Analysis
Audio?
Audio 데이터를 다루기 위해선, audio가 무엇인지 어떻게 표현되는지 알아야한다.
기본적으로, audio는 어떤 물체가 진동하면서 발생한다. 예를 들어 목소리의 경우 공기 분자가 진동을 하면서 발생한다. 즉 매질인 공기 분자가 얼마나 크게 흔들렸는지에 따라 형성되는 이러한 공기압의 진폭이, waveform 형태를 띄게 되어 우리가 흔히 보는 그래프가 그려진다.

Y축은 Amplitude(진폭), X축은 Time(sec) 이다.
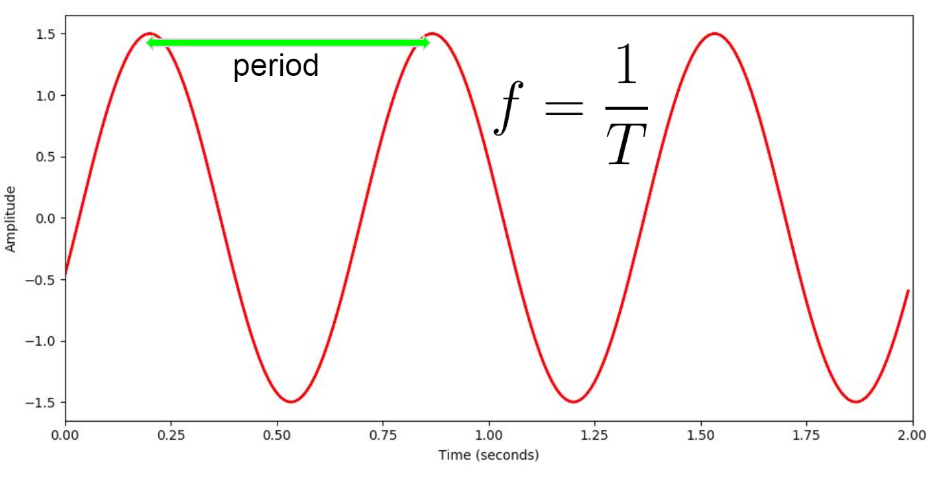
특정 지점에서 다음 등장하는 그 값까지를 period(주기)라고 정의한다. 이는 frequency(주파수) 개념으로 확장된다. Frequency는 Hz 단위를 사용하며, 1초에 100번 period(주기)가 발생하는, 즉 100번 진동하는 소리를 100Hz로 정의한다. 그래서 f = 1/T 라는 수식이 성립한다. 사람의 가청 Frequency는 약 20Hz ~ 20KHz.

High frequency, 즉 초당 진동 수(주기)가 많은 소리의 경우 High pitch(높은 소리)를 가진다. Amplitude는 소리의 크기(Loudness)와 관련되어 있다. 선형적이진 않지만, 대체로 Amplitude가 크면 소리가 크다.
Analog Digital Conversion(ADC)

오디오 데이터는 연속형 데이터이다. 이를 딥러닝에 input으로 넣기 위해선 discrete한 벡터로 만들어야 한다. 이를 위해, Analog digital conversion 과정을 거쳐야하고, 이는 Sampling과 Quantization 두 step으로 이루어진다. Sample rate는 초당 sample 갯수를 의미한다. 예를 들어, Sample rate = 44100Hz인 소리의 경우 1초에 44100개의 sample을 뽑았다는 말이다. Sample rate와 관련 된 법칙으로 Nyquist law가 있다. 모든 신호가 그 신호에 포함된 최고 주파수의 2배에 해당하는 빈도를 가지고 일정한 간격으로 샘플링하면 원래의 신호를 완벽하게 기록할 수 있다는 법칙이다. 사람의 가청 주파수(20Hz ~ 20KHz)의 최고 주파수인 20KHz의 2배인 40KHz에 오차 허용 범위 10% 및 영상 업계 표준과의 동기화 문제 등으로 인해 대부분의 오디오 sample rate는 44100Hz 값을 갖게 된다.
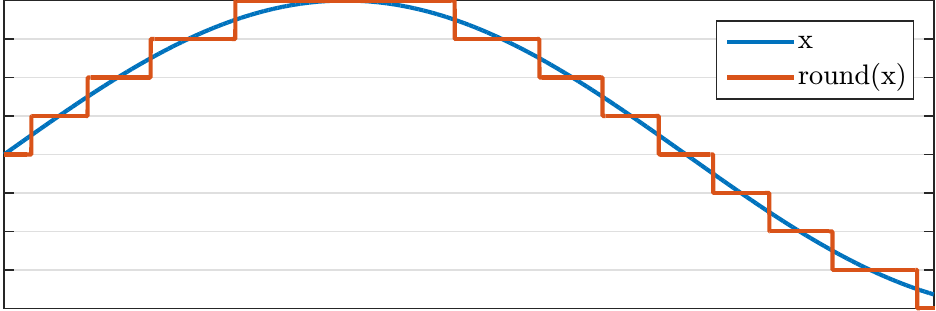
Quantization(양자화)은 위에 그림과 같이 continuous 한 sample 값들을 discrete value로 근사시키는 과정이다. 이와 관련된 개념으로 Bit depth가 있다. Bit depth는 quantization을 얼마나 세밀하게 할지에 대한 정도로, 예를 들어 오디오 파일의 Bit depth = 16bits 이면, 16 비트(약 65536 levels)의 값으로 dicrete하게 양자화 된 소리임을 의미한다. 양자화를 마친 데이터는 인코딩을 거쳐 '0'과 '1' 이진 비트로 표현된다. N개의 비트 한 세트를 PCM word라고 한다.
Feature extraction
오디오가 어떻게 정의되고, 데이터화 되는지 알아보았다. 하지만 오디오 데이터는 매우 고차원이고 여러 frequency가 섞여서 발생하므로, 데이터를 그대로 사용하기 보다는 신호의 성질을 잘 반영하는 feature를 뽑는 편이 좋다. 다음은 MFCCs(mel-frequency cepstral coefficients) 라는 가장 대표적인 오디오 feature를 뽑는 과정이다.

하나씩 알아보자.
Windowing(framing)
인풋 데이터인 오디오는 sequential하고, time dependent하다. 따라서 Time invariant(stationary) 가정이 가능해지는 아주 짧은 구간으로 신호를 쪼갠다. 이 과정을 Windowing이라고 한다. 이렇게 잘린 구간 내에서 신호는 stationary 가정을 만족해 시간에 영향을 받지 않게 된다. 음성인식 task에서는 각 구간이 하나의 phone을 가지게 잘라준다. 보통 25ms 정도를 한 구간 길이로 잡는다.
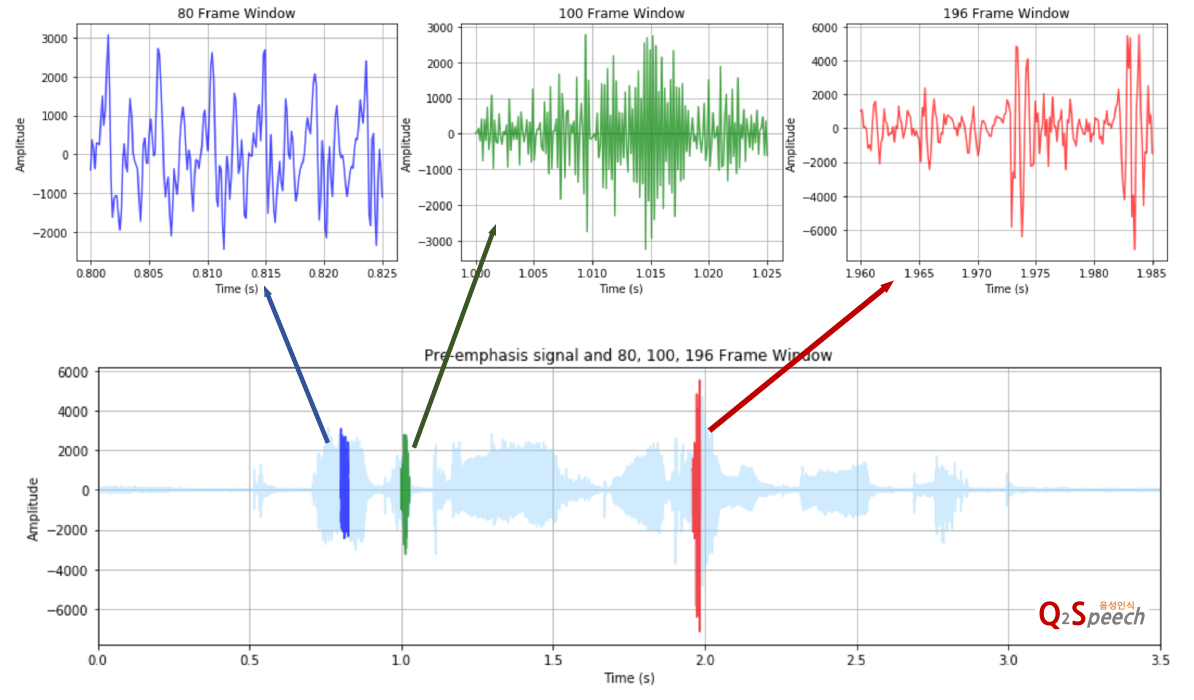
그런데, 이 때 구간의 경계(양 끝값)가 불연속해져 뚝뚝 끊기게 되어 실제 신호와 달라지는 문제가 생긴다. 이렇게 windowing이 신호 특성에 주는 영향을 최소화 하기 위해 양 경계값을 0으로 수렴시키는 window function을 각 구간(frame)마다 곱해준다. 다음 그림에 정규분포같이 생긴 함수가 window function이다.

Energy
energy는 waveform이 가지고 있는 에너지 값을 의미한다. 즉 signal의 전체 amplitude에 대응되는 값이다. signal의 각 amplitude 포인트를 $x_n$ 이라고 할 때, signal의 energy는 다음과 같이 정의된다.
$\sum_{n}^{}\left | x(n) \right |^2$
또, 많이 쓰이는 root-mean-square energy(RMSE)는 다음과 같다.
$\sqrt{\frac{1}{N}\sum_{n}^{}\left | x(n) \right |^2}$

RMSE는 나중에 MFCC feature 중 하나로 사용된다.
'Audio & Speech' 카테고리의 다른 글
| [음성인식] 5.2 Gaussian Mixture Model(GMM) (3) | 2020.04.08 |
|---|---|
| [음성인식] 4.3 Baum–Welch algorithm (1) | 2020.04.02 |
| [음성인식] 4.2 Hidden Markov Model (0) | 2020.04.02 |
| 오디오 데이터 전처리 (5) MFCC (7) | 2020.03.25 |
| 오디오 데이터 전처리 (2) Fourier Transform & Spectrogram (2) | 2020.03.25 |



