[음성인식] 5.1 Vector Quantization(VQ)에서 이어지는 글입니다. HMM을 음성인식에 적용하기 위해 방출 확률(emission probability)을 모델링하는 방법을 알아보고 있습니다. 지난 글에서 알아본 VQ에 이어 이번에는 Gaussian Mixture Model(GMM)입니다.
Guassian Mixture Model은 대표적인 비지도학습(unsupervised learning) 알고리즘 중 하나로 clustering과 유사한 논리 과정을 보인다. 비지도 학습은 라벨링이 안 된 데이터로 어떤 특성이나 규칙성을 찾아가는 머신러닝 학습 방법이다. GMM 공부에 선행되는 내용들을 정리한 뒤 다음 순서에 따라 논의를 전개하겠다.
1. Mulitnomial Distribution(다항분포)
2. Multivariate Gaussian Distribution(다변량 정규분포)
3. Gaussian Mixture Model
4. GMM for Speech Recognition
Mulitnomial Distribution
다항분포는 이름 그대로 이항분포의 다차원으로 확장이다. 동전 던지기(H, T)와 같은 시행이 이항분포를 따른다는 것은 우리 모두 익숙히 알고 있다. 이항분포가 '이'항 분포인 이유는 한 번 시행에 관측 가능한 값이 총 2개이기 때문이다. 다항분포도 이와 같은 논리를 따른다. K차원 다항분포는 한 번 시행에 관측 가능한 값이 총 K개인 시행을 N번 독립 시행한 것을 모델링한 분포이다. 예를 들어 4지선다 25문제를 푼 데이터를 모델링한다고 할 때 이를 다항분포로 모델링하고, K=4, N=25로 다항분포의 모수(parameter)를 정해줄 수 있다.
특정 시행에서 총 k개의 관측값이 나타날 수 있고 각각의 값이 나타날 확률을 $p_1,p_2, .... , p_k$ 라고 할 때, n번 시행에서 i번째 관측값이 $x_i$번 나타날 확률은 다음과 같고 이게 곧 다항분포의 pmf(확률질량함수)가 된다.
$f(X ; n,P) = \frac{n!}{x_1!x_2!...x_k!}p_1^{x_1}p_2^{x_2}...p_k^{x_k}$
$where, \sum_{i=1}^{k}x_i = n$ , $X = x_1,x_2,..,x_k$ , $P = p_1,p_2,..,p_k$
비슷한 분포인 베르누이 분포, 이항분포와 비교해보면 다음과 같다.
베르누이 분포 : 동전을 던져 앞면이 나올 확률
이항분포 : 주사위의 k번째 면이 n번 나올 확률
다항분포 : 주사위는 k_1, k_2, k_3 번째 면이 각각 n번 나올 확률
Maximum Liklihood Estimator(MLE)
위 수식에서도 알 수 있듯이 다항분포의 모수(parameter)는, 데이터(시행) 수 n과 각 관측값의 확률 P이다. 당연히 P는 관측 가능한 총 관측값 개수(k)만큼 있을 것이다. 이때 모수 P를 추정해보자. 통계에서 모수를 추정하는 다양한 방법이 있지만 여기서는 Maximum Likelihood Estimator(MLE)로 추정값을 사용하겠다. 또한 P 대신 일반적인 모수를 지칭하는 $\theta$를 사용하겠다. MLE는 특정 데이터가 주어졌을 때 가장 적합한 모수(parameter)를 추정하는 점 추정(point estimator) 방법 중 하나이다. MLE에 대한 자세한 내용은 다른 글에서 다루도록 하겠다. 우선 다항분포의 likelihood function을 구해야 한다. 다음은 각각 다항분포의 likelihood function과 log-likelihood function이다.
$L(\theta ; X ) = \prod_{k=1}^{K} \theta_k^{\sum_{n=1}^{N}x_nk}$
$if, m_k = \sum_{n=1}^{N}x_nk$
$l(\theta ; X ) = \sum_{k=1}^{K}m_k\ln\theta _k$
log-likelihood를 최대화하는 $\theta$를 찾으면 된다. 하지만 다항분포는 다음의 제약식이, $\sum_{i=1}^{k}x_i = n$ 있으므로 라그랑주 승수법을 이용하여 처리한다.
이후 세타에 대해 미분하고 그 값을 0으로 놓고(극값) 세타에 대해 정리하면, 다음과 같이 다항분포 모수 세타에 대한 MLE를 구할 수 있다.
$\theta_k^{MLE} = \frac{m_k}{N}$
Multivariate Gaussian Distribution
정규분포, 가우시안 분포는 수학자 가우스가 제시해 가우시안 분포라는 이름이 붙었다. 정규분포는 연속 확률 밀도함수(probability density function)의 한 종류로 평균 $\mu$와 분산 $\sigma^{2}$ 을 모수(parameter)로 가지는 확률분포이다. 정규분포의 pdf는 다음과 같다.
$f(x ; \mu ,\sigma^{2}) = N(x ; \mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi}\sigma}\exp (-\frac{(x-\mu)^2}{2\sigma^2})$

다변량 정규분포는 언급한 정규분포를 다차원으로 확장한 분포이다. 즉 인풋 데이터가 확률 변수가 아닌 확률 벡터로 주어진다. D차원 다변량 정규분포에서 parameter는 D차원 평균 벡터 $\mu$와, $D x D$ 차원 공분산 행렬 $\Sigma$를 갖는다. 이외에는 단변량 정규분포와 동일하다. 다변량 정규분포의 pdf는 다음과 같다. ( $\boldsymbol{\left | \Sigma \right |}$ 는 행렬식(determinant)을 의미한다)
$f(\boldsymbol{X} ; \boldsymbol{\mu} ,\boldsymbol{\Sigma}) = N(\boldsymbol{X} ; \boldsymbol{\mu} ,\boldsymbol{\Sigma}) = \frac{1}{(2\pi)^{D/2}\boldsymbol{\left | \Sigma \right |^{1/2}}}\exp \left \{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right \}$
Covariance Matrix
다변량 정규분포에서 주의 깊게 살펴볼 부분은 공분산 행렬(covariance matrix) $\Sigma$이다. 이 행렬이 다변량 정규분포의 형태를 결정하기 때문이다. 공분산 행렬의 (i, i) 원소는 i 차원의 분산, (i, j) 원소는 i와 j 차원의 공분산을 의미한다. 따라서 symmetric이며 positive-definite matrix이다. 서로 다른 공분산 행렬을 가지는 2변량(차원) 정규분포인 다음 그림을 보자.
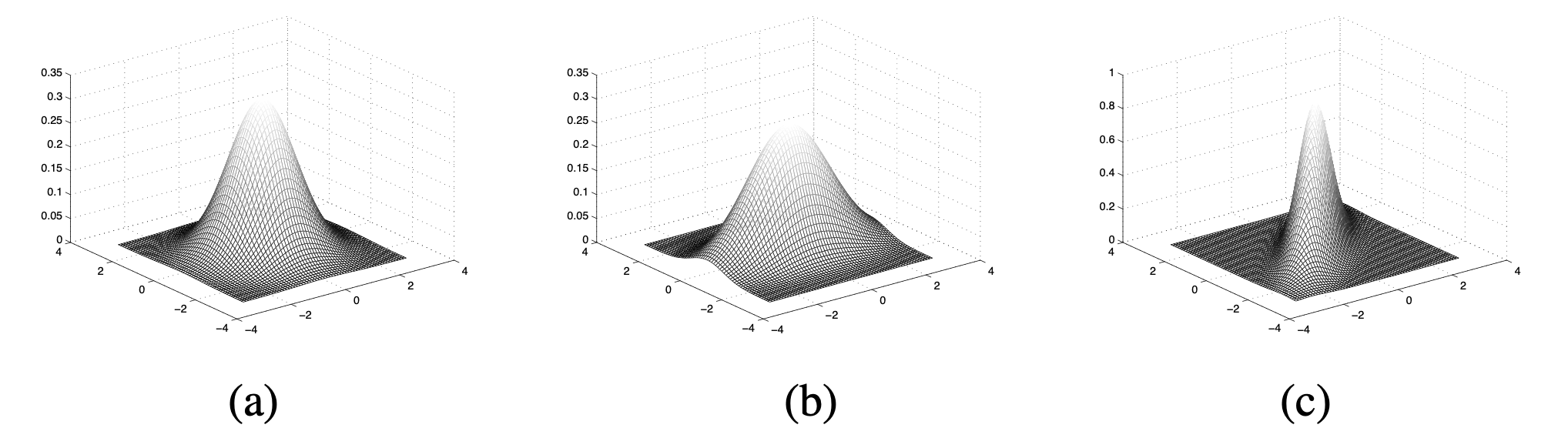
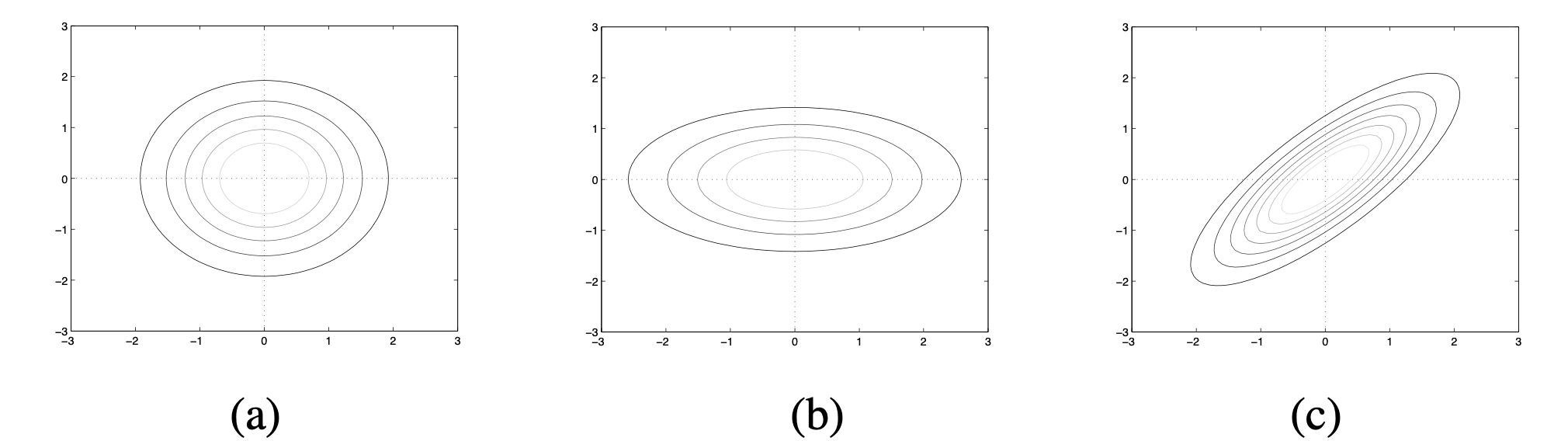
(a)는 두 차원의 분산이 동일하고 공분산이 없는 경우다. 따라서 다음과 같은 공분산 행렬을 가지게 된다.
$\Sigma_a = \begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}$
(b)는 한 쪽 차원의 분산이 다른 쪽에 비해 큰 경우다. 다음과 같은 공분산 행렬을 가진다.
$\Sigma_b = \begin{pmatrix}
0.5 & 0\\
0 & 2
\end{pmatrix}$
(c)는 분포가 축 방향으로 정렬되어 있지 않고, 이는 각 차원이 공분산을 가진다는 것을 의미한다. 다음과 같은 공분산 행렬을 가진다.
$\Sigma_c = \begin{pmatrix}
1 & 0.8\\
0.8 & 1
\end{pmatrix}$
Maximum Liklihood Estimator(MLE)
다변량 정규분포의 paremeter를 추정해보자. D차원 다변량 정규분포의 parameter는 D차원 평균 벡터 $\mu$와, $D x D$ 차원 공분산 행렬 $\Sigma$ 이다. 이를 추정하기 위해 MLE를 사용한다. 우선 log-likelihood function을 구한다.
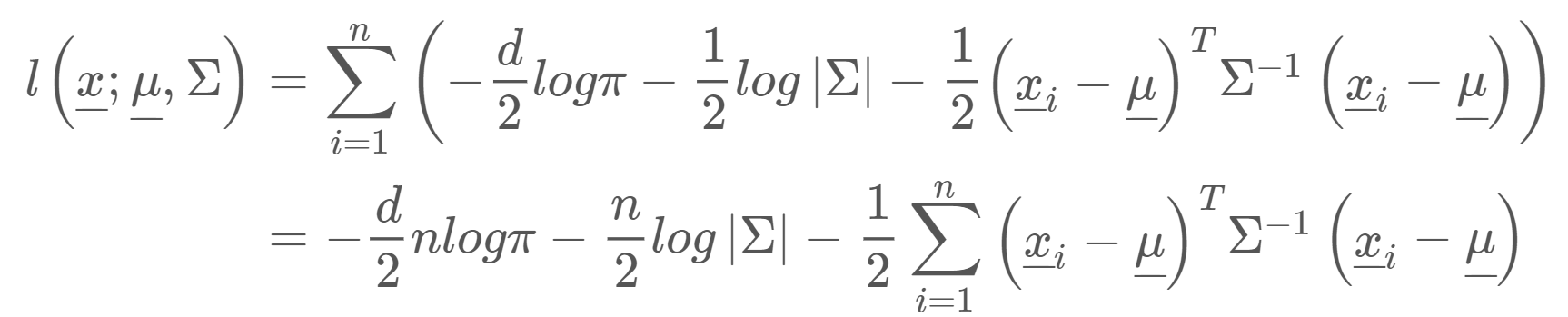
이 함수를 최대화시키는 게 목적이므로 추정하고자 하는 parameter에 대해 각각 편미분을 해준다. 우선 $\mu$에 대해 편미분 해보자.
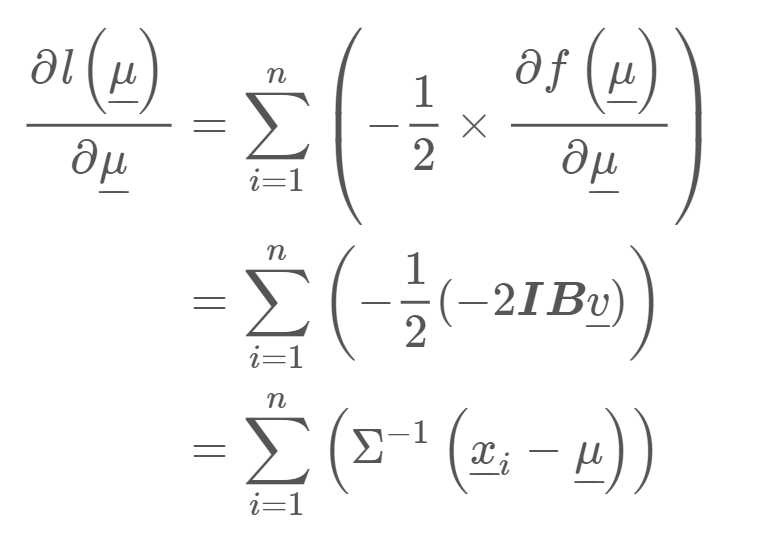
이후 그 값을 0으로 두고 $\mu$에 대해서 정리하면, 다변량 정규분포의 첫 번째 parameter인 $\mu$의 MLE 추정값을 다음과 같이 구할 수 있다.
$\widehat{\boldsymbol{\mu}}^{MLE} = \frac{\sum_{i=1}^{n}\boldsymbol{X}_i}{n}$
다변량 정규분포의 두 번째 parameter인 $\boldsymbol{\Sigma}$에 대해서도 위와 같이 MLE로 추정할 수 있다.
Gaussian Mixture Model
자, 이제 GMM을 공부하기 위한 준비가 끝났다. GMM은 M개의 서로 다른 정규분포의 가중합으로 데이터를 표현하는 모델이다. GMM을 이루는 개념들을 하나씩 살펴보자.
Mixture Model
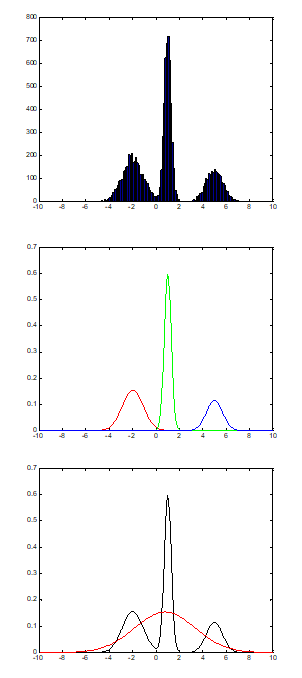
데이터 히스토그램을 찍었는데 첫 번째 그림과 같이 나왔다고 생각해보자. 정규분포 하나로 모델링 하기에는 부족해 보인다. 그러면 두 번째 그림처럼 서로 다른 정규분포 3개(빨강, 초록, 파랑)로부터 데이터가 나왔다고 생각해, 그 세 분포의 mixture distribution(혼합분포)으로 모델링하는 방법은 어떨까? 바로 이게 Mixture Model의 기본 아이디어다. 그중 GMM은 혼합 분포로 쓸, 각 sub 분포들을 정규분포로 가정하는 모델이다.
Gaussian Mixture Model
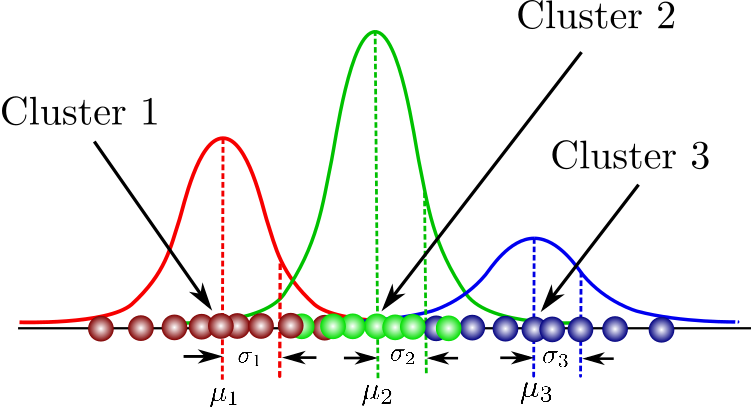
GMM의 개념은 mixture model과 동일하지만 sub 분포를 정규분포로 사용하는 모델이다. 위 그림은 3개의 sub 분포를 가지는 GMM이다. GMM은 데이터가 어떤 분포로 assign 될지에 관심이 있으므로 clustering과 유사한 논리 과정을 가진다. 모든 k번째 sub 분포는 $\pi_k$라는 가중치를 가지고 weighted sum으로 다음과 같이 GMM을 구성한다. GMM의 parameter는 $\theta = (\pi_k, \mu_k, \Sigma_k) , k = i, ... , K$ 이다.
$f(\boldsymbol{X} ; \theta) = \sum_{k=1}^{K}\pi_k N(x|\boldsymbol{\mu_k}, \boldsymbol{\Sigma_k})$
여기서 $\pi$는 각 분포의 가중치이고, Z라는 새로운 다항분포를 도입해 다음과 같이 모델링한다.
$z_k \in \left \{ 0,1 \right \},\sum_{k}^{} z_k = 1$
$P(z = 1) = \pi_k , \sum_{k=1}^{K}\pi_k =1$
$P(Z) = \prod_{k=1}^{K}\pi_k^{z_k}$
이를 통해, k번째 분포에서 주어진 데이터가 관측될 확률은 다음과 같이 구할 수 있다.
$f(X | z_k = 1) = \prod_{k=1}^{K} N(x|\mu_k,\Sigma_k)^{z_k}$
그렇다면 특정 데이터가 주어졌을 때 k번째 분포로 assign 될 assignment probability를 베이즈 정리를 활용해 다음과 같이 구할 수 있다.
$\gamma (z_nk) = P(z_k = 1|x_n) = \frac{P(z_k=1)P(x|z_k = 1)}{\sum_{j=1}^{K}P(z_j=1)P(x|z_j=1)}$
$= \frac{\pi_kN(x|\mu_k,\Sigma_k)}{\sum_{j=1}^{K}\pi_jN(x|\mu_k,\Sigma_j)}$
다음으로는 GMM의 log-likelihood function을 구해보자. (왜 구하는지는 조금 이따 알게 된다!)
$l(\theta ; X) = \sum_{k=1}^{K}\ln \left \{ \sum_{k=1}^{K}\pi_kN(x|\mu_k,\Sigma_k) \right \}$
$where, \theta = (\pi_k, \mu_k, \Sigma_k) , k = i, ... , K$
Estimating GMM(E-M algorithm)
GMM이 어떤 모델인지 알아봤으니 이를 estimating 하는 과정을 알아보자. 통계적 추정(statistical estimating)은 최근 각광받는 딥러닝에서 모델이 데이터를 학습한다고 해서 learning이라고 부르기도 한다. 추정 방법으로는 MLE의 응용인 E-M algorithm을 사용한다. E-M은, 각각 expectation과 maximization의 약자로 두 과정을 반복하며 likelihood를 최대화시키는 알고리즘이다.
먼저 Expectation부터 보자. GMM의 expectation 단계에서는 데이터 X와 parameter $\theta = (\pi_k, \mu_k, \Sigma_k) , k = i, ... , K$ 가 주어졌을 때 assignment probability를 구한다. 위에서 구한 공식을 사용하면 된다! K-mean clustering에서 특정 cluster로 데이터가 assign 될 확률을 구하는 과정과 동일하다. 초기값으로는 당연히 랜덤값을 주고 학습을 시작한다. 결론적으로 expectation 단계에서는 새로운 assignment probability를 구한다.
다음 maximization 단계에서는 expectation 단계에서 구한 assignment probability를 가지고 GMM parameter $\theta = (\pi_k, \mu_k, \Sigma_k) , k = i, ... , K$ 를 업데이트한다. 업데이트에 MLE를 적용하므로 위에서 구해둔 log-likelihood를 여기서 사용한다. 앞선 논의대로 log-likelihood를 각 parameter에 대해 편미분 해 MLE를 구하면 다음과 같다.
$\widehat{\mu_k}^{mle} = \frac{\sum_{n=1}^{N}\gamma (z_nk)x_n}{\sum_{n=1}^{N}\gamma (z_nk)}$
$\widehat{\Sigma_k}^{mle} = \frac{\sum_{n=1}^{N}\gamma (z_nk)(x_n-\widehat{\mu_k})(x_n-\widehat{\mu_k})^{T}}{\sum_{n=1}^{N}\gamma (z_nk)}$
$\widehat{\pi_k}^{mle} = \frac{\sum_{n=1}^{N}\gamma (z_nk)}{N}$
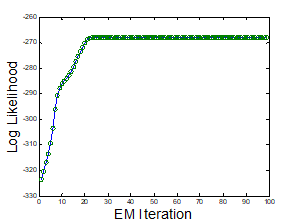
이렇게 구한 MLE 값으로 parameter를 업데이트해주면 한 번 iteration(E-M)을 돈 게 된다. 여러 번 반복하면 다음과 같이 학습이 진행된다. 총 99번 E-M iteration을 돌린 GMM이다.
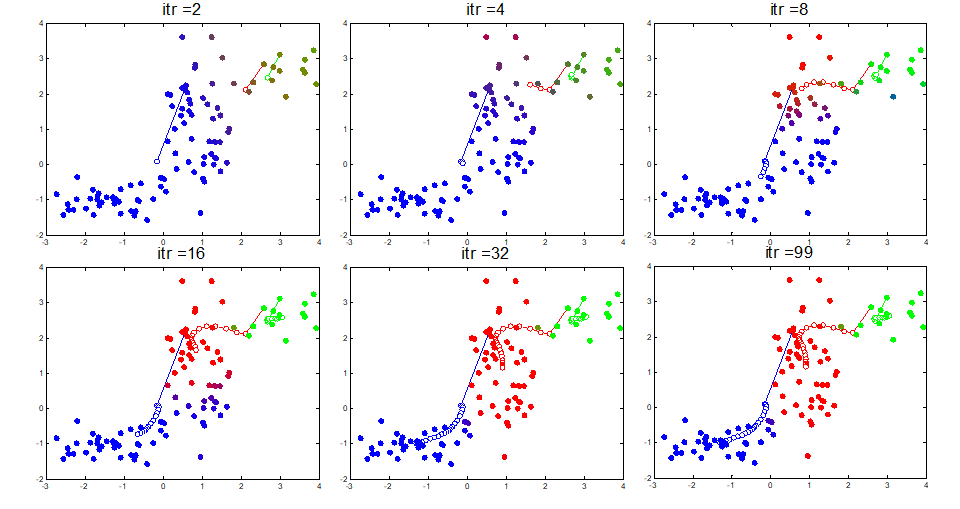
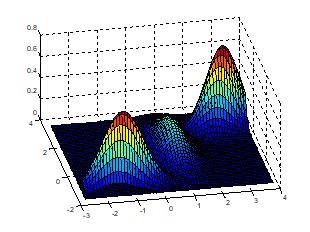
그림을 보면 초기에는 색이 불명확한 데이터 포인트들이 보이고 clustering도 거의 되지 않은 모습이다. 학습이 반복되면서 점점 경계에 불명확한 데이터들이 줄어들고 clustering 구조가 잡혀가는 것을 확인할 수 있다. 아래 그래프를 보면 E-M iteration이 돌수록 log-likelihood 값이 증가해 수렴하는 것을 알 수 있다.
GMM for speech recognition
GMM이 무엇인지, 어떻게 학습되는지도 알았으니 음성인식 task로 돌아와 GMM이 음성인식에 어떻게 적용되는지 알아보자. 우리는 결국 GMM을 사용해서 HMM 각 state가 주어졌을 때 acoustic feature의 관측 확률(emission prob)을 구하고자 한다. 음성인식에서의 acoustic feature인 MFCC는 39차원이다. 따라서 39차원 다변량 정규분포를 sub 분포로 가지는 GMM으로 모델링을 한다.
$b_j(o_t) = \frac{1}{(2\pi)^{\frac{D}{2}}\left | \Sigma \right |^{\frac{1}{2}}}\exp (-\frac{1}{2}(o_t-\mu_j)^{T}\Sigma_j^{-1}(o_t-\mu_j))$
여기서 고려해야 할 부분이 하나 있다. 39차원 다변량 정규분포이기에 39 x 39 공분산 행렬이 있다. 이 공분산 행렬을 Full로 가정하면 연산량이 너무 많다. 따라서 diagonal 공분산 행렬을 사용하는 것이 계산 효율적이다. 따라서 실제 음성인식 모델링에서 인풋 feature(MFCC) decorrelation이 요구된다. (eg. fundemental frequency 앞쪽 제거를 통한 화자 정보 제거)
그럼 그냥 39차원 다변량 정규분포로 모델링하면 되지 왜 GMM을 사용하냐는 의문이 들 수 있다. 음성 신호가 가지는 다양한 보이지 않는 특성(latend factor)들을 비지도 학습인 GMM을 통해 찾아낼 수 있기 때문이다. 예를 들어 어떤 음성 신호가 무성음과 유성음으로 구성되어 있다고 하자. 하지만 우린 그 정보를 모르는 상태다(latent factor). 이때 GMM을 통해 신호를 무성음과 유성음으로 clustering 시켜 latent factor detection 효과를 얻을 수 있다.
HMM-GMM
이때까지 음성인식 acoustic modeling에 사용되는 HMM-GMM 내용을 여러 글에 걸쳐 정리해보았다. 4.1 Acousitc Model (HMM-GMM)에서 알 수 있듯이 음성인식은 크게 AM, LM 두 가지 모델로 구성된다.
$\widehat{W} = argmax_{w\in L} P(O|W)P(W)$
여기서 P(O|W)가 acousitc model(AM)이고 P(W)가 language model(LM)이다. HMM-GMM은 여기서 AM에 사용된다. HMM은 phones sequence가 주어졌을 때의 특정 word가 관측될 확률을 계산하고, GMM은 이 HMM의 방출 확률(emission probability)을 계산하는 데 사용된다. 예를 들어 다음과 같이 'she just had ~'라는 음성 신호를 HMM-GMM으로 모델링한다고 해보자.

이 문장(or 단어)은 하나의 HMM으로 구성되고 HMM, sub-phones을 hidden state 값으로 가진다. 각 state의 phone에 대응하는 acousitc feature(MFCC)가 관측될 확률(emission prob)을 GMM으로 구한다. GMM은 각 state마다 하나씩 있어야 하므로 HMM hidden state 개수만큼 존재해야 한다.
'Audio & Speech' 카테고리의 다른 글
| 오디오 데이터 전처리 (1) Waveform (7) | 2020.04.02 |
|---|---|
| [음성인식] 4.3 Baum–Welch algorithm (1) | 2020.04.02 |
| [음성인식] 4.2 Hidden Markov Model (0) | 2020.04.02 |
| 오디오 데이터 전처리 (5) MFCC (7) | 2020.03.25 |
| 오디오 데이터 전처리 (2) Fourier Transform & Spectrogram (2) | 2020.03.25 |



