Deep Learning, Ian Goodfellow(www.deeplearningbook.org/) 공부하고 정리한 글입니다.
내용을 함께 고민해 준 KAIST 김현우, 최정만에게 감사합니다.
대부분의 머신러닝 알고리즘은 해석적 방법이 아닌 반복을 통해 추정하는 최적화 문제로 알고리즘을 푼다. 하지만 디지털 컴퓨터의 유한한 비트 메모리로 무한한 실수를 정확하게 표현할 수 없기에 생기는 문제들이 있다.
1. Overflow, Underflow
컴퓨터의 비트 표현으로는 실수를 정확히 표현할 수 없어, 반올림을 통한 근사표현을 한다. 이때, 0에 가까운 수가 반올림에 의해 정확히 0이 되는 것을 underflow, 매우 큰 수가 반올림되어 $\infty, -\infty$가 되는 것을 overflow라고 한다. 이로 인해 0으로 나누기 등 여러 문제가 발생할 수 있으므로 underflow, overflow에 대한 안정화가 필요하다. 이는 대부분 라이브러리에 구현되어 있다.
2. Poor Conditioning
조건화(conditioning)는 입력의 작은 변화에 함수가 얼마나 급하게 변하는지를 나타낸다. 즉 조건수가 크면, 조건화가 나쁘고 입력 수치 오차에 민감하다. $f(x) = A^{-1}x$에서 고유값 분해가 존재하는 행렬 $A$의 조건수(condition number)는 가장 큰 고유값과 가장 작은 고윳값의 크기 비로 정의한다.
$max\left | \frac{\lambda _{large}}{\lambda _{small}} \right |$
3. Gradient based optimization
머신러닝은 해석적 최적화 대신 수치적으로 x 값을 바꿔가며 f(x)를 최소화한다. f(x)는 objective function, 최소화하는 관점에서 cost/loss function이라고도 한다. 이 때, gradient의 역방향으로 f(x)값을 updt하며 최소화하는 방법이 gradient descent.
Jacobian
입력과 출력이 모두 벡터인 다차원 함수의 1차 편미분 jacobian, 2차 편미분 hessian. 2차 미분값은 입력에 따라 gradient가 얼마나 변하는지(곡률) 알려준다. 이는 함수의 convexity 판정 외에도 gradient descent의 한 step이 얼마나 해를 개선하는지 알려준다. 예를 들어, gradient가 1인 이차 미분값이 음수, 0, 양수인 경우를 살펴보자.
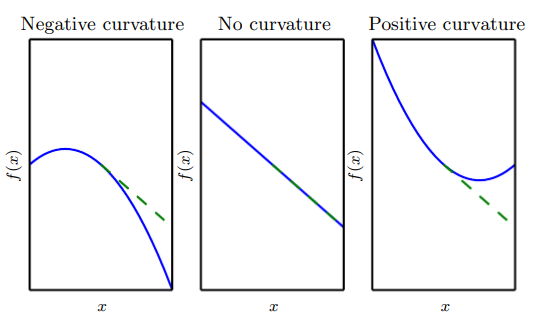
이차 미분값이 음수면 해당 지점 근처에서 concave한 형태를 가지며, gradient descent의 한 step이 gradient보다 더 이동한다. 0인 경우 gradient 만큼 이동하게되고, 양수인 경우 gradient 보다 덜 이동하게 된다.
Hessian
hessian은 다차원 함수의 이차 편미분을 모아둔 행렬이다. 이차 미분값이 존재하고 연속인 함수에 대해 hessian은 항상 symmetric 하며, orthogonal eigenvector로 decompostition 가능하다. Hessian을 이용해 gradient descent에 2차 미분을 반영할 수 있다. 우선 f(x)를 2차 테일러 근사 시킨다.
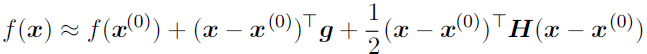
여기서 gradient descent 알고리즘 $x = x - \varepsilon g$를 대입하면 다음과 같다.
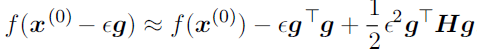
이 때, 첫번째 텀은 함수의 원래 값, 두번째 텀은 gradient로 updt할 값, 세번째 텀은 앞서 살펴 본 곡률에 한 오차를 보정하기 위한 값이다. $\varepsilon$이 양수일 때, 두번째 텀은 항상 양수이므로, $g^THg$가 0이나 음수 일때 f는 영원히 감소한다. 반면 $g^THg$가 양수면 f를 가장 많이 감소시키는 최적의 $\varepsilon$이 존재한다.

헤시안 행렬과 고윳값, convexity에 관한 내용은 따로 정리했다.
Hessian 행렬과 Positive-Definite
Definite 정의 $f(x) = X^TAX = a_{11}x_1^2 + 2a_{12}x_1x_2 + \cdot \cdot +a_{nn}x_n^2, \ X\in \mathbb{R}^n$ 위와 같이, n개 변수를 갖는 quadratic form 함수 f(x)가 있을 때, 극점 x = 0을 제외한 모든 x..
hyunlee103.tistory.com
4. Constrained Optimization
어떤 집합 S에 속한 x의 값들에 대해서 objective function f(x)를 최적화하는 문제. 이때, x를 feasible point라고 한다. 제약있는 최적화 문제는 constrained optimization을 같은 방향의 unconstrained optimization으로 치환하는게 핵심이다.
'ML & DL' 카테고리의 다른 글
| [NLP] ELMo, Contextual Word Representation (0) | 2021.02.10 |
|---|---|
| [NLP] Language Model, Seq2Seq, Attention (0) | 2021.02.10 |
| [Deep learning] 8장 최적화 ① (1) | 2021.01.14 |
| [Deep learning] 3장 확률론과 정보 이론(probability, information theory) (0) | 2021.01.14 |
| [Deep Learning] 2장 선형 대수 (0) | 2021.01.10 |


