Deep Learning, Ian Goodfellow(www.deeplearningbook.org/) 공부하고 정리한 글입니다.
많은 내용을 함께 고민해준 KAIST 김현우, 최정만에게 감사합니다.
1. Training vs Optimization
머신러닝은 성과 측도 P(고양이, 개를 얼마나 잘 분류하는지)를 좋게하는게 목표인데, 직접 P를 평가하기 어려워 학습과정에서 loss 최소화하는 간접적인 방법을 사용한다. 전통적인 최적화는 loss를 최소화 하는 것 자체가 목표다. loss의 기댓값을 risk function이라고 하고 다음과 같이 표현한다.
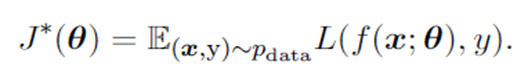
이때, $p_{data}$ 분포를 알면 순수 최적화 문제지만, 전체 데이터 분포를 모르는 머신러닝은 sample로 추정한 $\hat{p}_{data}(x,y)$ 분포를 이용해 risk function 대신 empirical risk를 최소화한다. 그러나 overfitting, 미분 불가한 loss 함수 등 문제로 딥러닝에서는 empirical risk minimization을 사용하지 않는다.
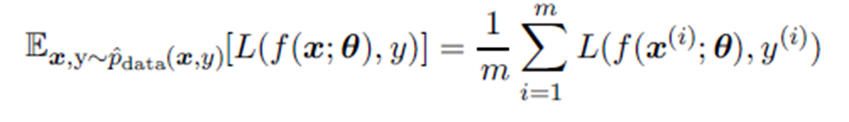
따라서 딥러닝에서는 미분가능한 surrogate loss function을 사용한다. 정답 y의 negative log likelihood가 대표적인 surrogate loss. 이를 통해 데이터 x가 주어졌을 대 정답 y에 대한 조건부 확률을 추정한다. 순서 최적화 알고리즘은 gradient가 0에 수렴하면 종료하지만, 학습 알고리즘은 val set에 대한 수렴이 판정되면 종료한다. 순수 최적화와 달리 train set loss의 극소점에서 종료 될 필요도 종료되지도 않는다.
Batch
Batch는 원래 train data set 전체를 의미하고, mini-batch가 sub set을 의미하지만, 둘 다 sub set 의미로 사용하기도 한다. 딥러닝은 배치 단위로 파라미터를 추정(학습)하는데, n개 sample로 추정한 파라미터 평균의 표준편차는 $ \frac{\sigma}{\sqrt{n}}$ 이므로 배치 사이즈 증가에 따른 추정치 분산이 선형적으로 줄어들지 않아 효율이 떨어진다. 즉 배치가 클수록 gradient 추정값은 정확하지만, 커지는 만큼 정확해지지 않는다. 한편, 작은 배치 사이즈는 regularizaiton 효과를 줄 수 있다. 이때 learning rate는 낮게 설정하는게 좋다.
알고리즘에 따라 sampling error 민감도가 다르다. 1차 최적화인 gradient 기법은 추정할 파라미터가 상대적으로 적으므로 작은 배치크기를 사용해도 괜찮다. 반면 2차 최적화는 헤시안을 사용하므로 추정할 파라미터가 많고, 특정 에러가 큰 변동으로 이어지므로 상대적으로 정확한 추정값이 필요해 배치 크기가 크면 좋다.
Mini-batch stochastic gradient descent는 같은 sample이 반복되지 않으면(비복원 추출의 경우) risk function의 불편 추정량이 된다. 하지만 적당한 복원 추출을 통해 생기는 bias는 모델 일반화에 도움이 된다.
2. Challenges in Neural Network Optimization
신경망 모델을 최적화하는데 발생할 수 있는 여러가지 이론적인 문제점들을 다룬다.
이러한 이론적 최적화 문제들은 실제 신경망 사용에 큰 영향을 주지 않는데, 일부 이론은 discrete function에만 해당되고(신경망은 contineous function), 신경망 최적화의 목표는 global minima가 아닌 cost 함수를 충분히 감소시켜 empirical risk를 줄이는 것이기 때문이다.
헤시안의 ill-conditioning
Local minima
Neural net의 cost function은 local minima가 엄청 많은 non-convex 함수다. 충분히 큰 신경망은 대부분의 local minima에서 cost가 최소는 아니더라도 충분히 작은 값을 갖는다.
충분한 데이터로 모델 파라미터의 구성 중 하나를 유일하게 결정가능한 모델을 Model identifiability 하다고 한다. 신경망의 경우 latent variables을 교환해서(단순 오토인코더에서, 인코더 layer와 디코더 layer를 교환한다고 생각해보자) equivalent한 모델을 얻을 수 있으므로 Not identifiability Model 이다. 오토인코더 같이 layer 단의 weight 구조를 서로 바꿔도 같은 모델을 weight space symmetry 하다고 한다.
Plateaus, saddle points, and other flat regions
saddle points는 cost 함수의 한 단면에서 local minima와 maxima가 일치하는 점이다. 헤시안의 eigen-value가 양수, 음수 섞여 있는 경우이다. cost 함수는 학습이 진행됨에따라 비용이 작은 영역에 접근하면서 헤시안 eigen-value가 양수가 될 확률이 커진다. 따라서 비용이 큰 임계점은 saddle point, 낮은 임계점은 local minima일 확률이 높다.
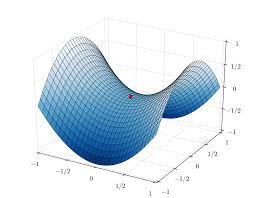
Gradient descent 같은 1차 최적화는 saddle point를 잘 넘어가지만 뉴턴 method 같은 2차 최적화는 상대적으로 saddle에 빠질 확률이 크다. 이는 단순히 함수가 내려가는 방향으로 설계된 gradient descent와 다르게 뉴턴 method는 기울기가 0인점을 명시적으로 구하게 설계 되었기 때문이다.
Cliffs and Exploding Gradients
큰 가중치들이 반복해서 곱해지는 깊은 비선형 신경망은(특히 RNN 계열) cost 함수 공간에 급한 비선형구간(아래 그림같은 절벽)이 존재하는 경우가 많다. 절벽에 가까워지면 gradient descent 갱신 단계에서 파라미터가 급격히 변해(gradient가 갑자기 커지므로) 이때까지의 최적화 결과가 무의미해지는 문제가 있다. Gradient clipping 등 weight normalizaion을 통해 이를 해결한다.
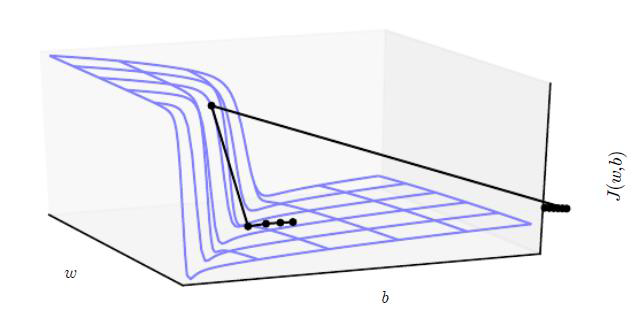
Long-term dependencies
가중치 $W$를 매 layer마다 반복하는 신경망(RNN 계열)의 경우 t번 layer를 거치면 $W^t$가 되고 이를 대각화 하면,
$W^t = (Vdiag(\lambda)V^{-1})^t = Vdiag(\lambda)^tV^{-1}$
이때, 특정 eigen-value 값이 1보다 크면 gradient exploding, 1보다 작으면 gradient vanishing이 발생한다. 이는 학습시 발생하는 gradient가 W의 eigen-value에 지수적으로 비례하기 때문이다. RNN 계열이 아닌 feed-forward network는 매 layer 마다 서로 다른 가중치를 사용하므로 위 문제에서 비교적 자유롭다.
Inexact gradient, Poor correspondence between local and global stucture
대부분의 최적화 알고리즘은 정확한 gradient를 구할 수 있음을 가정하지만, 실제론 배치로 추정해서 사용한다. 즉, 우리가 학습에 사용하는 gradient가 global stucture 관점에서 정확한 gradient가 아닐 수 있다.
또한 saddle, local point가 없어도 local surface에 수렴하는 문제가 있어 가중치 초기값 설정이 중요하다.

'ML & DL' 카테고리의 다른 글
| [NLP] Language Model, Seq2Seq, Attention (0) | 2021.02.10 |
|---|---|
| [Deep learning] 4장 수치 계산(Numerical Computation) (0) | 2021.01.18 |
| [Deep learning] 3장 확률론과 정보 이론(probability, information theory) (0) | 2021.01.14 |
| [Deep Learning] 2장 선형 대수 (0) | 2021.01.10 |
| [Deep learning] 6장 Deep Feedforward Network (0) | 2020.12.26 |

