Deep Learning, Ian Goodfellow(www.deeplearningbook.org/) 공부하고 정리한 글입니다.
많은 내용을 함께 고민해준 KAIST 김현우, 최정만에게 감사합니다.
1. Multiplying Matrices and Vectors
모든 행렬 선형 변환이자 함수다. 행렬, 벡터의 연산은 다음 세 가지가 대표적이다.
1) Matrix product: 행렬곱, 차원이 맞는 두 행렬의 곱 연산에 사용된다. $AB$
2) Element-wise product: 차원이 맞는 두 행렬을 동일한 위치의 원소끼리 곱한다. $A \odot B$
3) Dot product(내적): 행렬곱의 각 성분은 행렬을 구성하는 벡터들의 내적이다. $v^Tu$
내적은 교환법칙이 성립하지만 행렬곱은 교환 법칙을 사용할 수 없다. 선형대수학은 선형 방정식의 해 x를 찾는 것을 목표로 한다.
$Ax = b$
A의 역행렬이 존재한다면, 양변에 A의 역행렬을 곱해 x를 구할 수 있지만 실제 컴퓨터로는 역행렬을 근사적으로만 구할 수 있기에 잘 사용하지 않고, b를 활용하는 알고리즘으로 x를 추정한다.
2. Linear Dependence and Span
$Ax = b$
이 선형방정식의 해가 있는지는 b가 A의 column space에 속하는지로 판단한다. 즉 b가 A의 선형 결합으로 만들어질 수 있는지 보는 것이다. 행렬 A가 정방행렬이고 모든 column이 선형 독립이면 A의 역행렬이 존재하고, 모든 b에 대해 단 하나의 해(x)가 존재한다. 이러한 행렬 A를 non-singular matrix라고 하고, 반대로 행렬 A의 하나의 column이라도 선형 종속이면 singular matrix라고 한다. 선형 대수의 벡터에 대한 선형 독립과 통계학의 확률변수에 대한 독립은 헷갈리기 쉬워 따로 정리했다.
[Statistic] - 독립과 직교(orthogonal)
독립과 직교(orthogonal)
Independent와 orthogonal은 통계학을 공부하면서 계속해서 등장한다. 뭔가 비슷하면서도 다른 두 개념을 더 헷갈리게 하는 건 대상이 벡터인지 변수(variable)인지에 따라 의미가 달라지기 때문이다. 선
hyunlee103.tistory.com
3. Norms
Norm은 벡터의 크기를 측정하는 함수, 벡터를 음이 아닌 값으로 mapping 한다. 기하학적으로, 벡터 x의 norm은 해당 공간에서 origin(원점)으로부터 점 x까지의 거리를 의미한다. 일반적인 p-norm은 다음과 같이 정의한다.
$\left \| x \right \|_p = (\sum_{i}^{}\left | x \right |^p )^{\frac{1}{p}}$
p = 2일 때, Euclidean norm, L2 norm이라고 한다. 제곱이 벡터 자신과 내적과 같다. 가장 많이 쓰이는 norm이라 하첨자 2를 때고 쓰기도 한다.
$\left \| x \right \|_2 = \left \| x \right \| = \sqrt{\sum_{i}^{}x_i^2}$
p = 1일 때, L1 norm이라 하고, L2 보다 상대적으로 거리에 둔감하다.
$\left \| x \right \|_1 = \sum_{i}^{}\left |x_i \right |$
p = $\infty$일 때, max norm이라 하고 해당 벡터의 max값의 절댓값을 출력한다.
Frobenius norm, 행렬의 크기 구할 때 사용, L2 norm과 유사하다.
$\left \| A \right \|_F = \sqrt{\sum_{i,j}^{}\left |A_{i,j}^2 \right |}$
4. Special Kinds of Matrices and Vecters
Diagonal matrix: 대각행렬, 주대각 성분 빼고 0인 행렬이다. element-wise 하게 연산되므로 벡터와 곱 연산이 효율적이다. 모든 주대각 성분이 0이 아니면 역행렬이 존재하며, 주대각 성분을 역수 취한 형태이다.
$A=\begin{pmatrix} 2 &0 \\ 0 &3 \end{pmatrix}$
$A^{-1}=\begin{pmatrix}
\frac{1}{2}&0 \\
0 &\frac{1}{3}
\end{pmatrix}$
Symmetric matrix: 대칭행렬, Transpose가 자신과 동일한 행렬이다. $A^{T} = A$
Unit vector: L2 norm이 1인 벡터
Orthogonal: 두 벡터의 내적이 0일 때, 두 벡터는 orthogonal 하다고 정의한다. 두 벡터가 orthogonal 하면 선형 독립이지만, 선형 독립이라고 orthogonal 하지는 않다.
Orthogonal matrix: 모든 행과 열이 orthonomal(unit + orthogonal) 벡터인 정방행렬, transpose가 역행렬이 된다.
$A^{-1} = A^{T}$
5. Eigendecomposition(고윳값 분해)
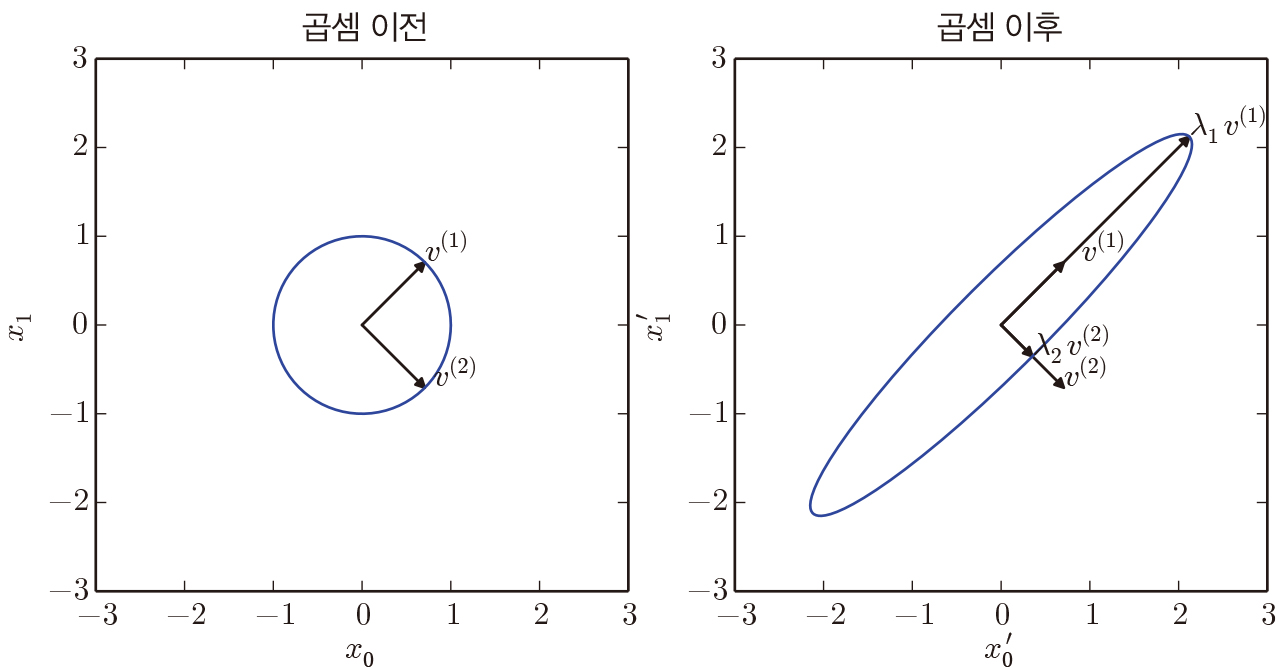
행렬을 분해하면 여러 잠재된 성질을 찾을 수 있다. 고윳값 분해는 정방행렬을 eigenvector와 eigenvalue로 분해한다. 다음 식의 $v$가 eigenvector $\lambda$ 가 eigenvalue다.
$Av = \lambda v$
행렬 $A$의 eigenvector는 $A$라는 선형 변환에 그 방향은 유지한 채 scale만 변하는 벡터이다. 이때 scale이 eigenvalue가 된다. 행렬 $A$의 고윳값 분해는 다음과 같고, eigenvalue $\lambda$를 내림차순으로 정렬한 대각행렬과 각 eigenvalue에 대응되는 eigenvector를 colunm으로 갖는 행렬 $V$와 그 역행렬로 분해된다. 일반적으로 eigenvector는 무수히 많아 L2 norm = 1로 정규화된 eigenspace의 basis를 사용한다. 또한 $V$ 역행렬이 존재해야 하므로, $V$의 colunm, 즉 eigenvector가 모두 선형 독립이어야 고윳값 분해 가능하다.
$A = Vdiag(\lambda)V^{-1}$
고윳값 분해 성질
1) A가 실수인 대칭행렬이면, eigenvalue는 항상 실수이고, eigenvector는 orthogonal 하다.
2) 행렬 A의 eigenvalue는 유일하고 eigenvector는 scalar배로 무수히 존재할 수 있다.
3) 행렬 대각 원소에 a만큼 더하면 eigenvalue값이 a만큼 증가하지만, eigenvector는 변하지 않는다.
4) 행렬 A의 모든 eigenvalue가 서로 다른 값을 가지면, 반드시 독립인 n개의 eigenvector를 갖고 고윳값 분해 가능하다.
5) 중복인 eigenvalue를 가지면 모두 독립인 eigenvector를 가질 수 있고(단위, 회전 행렬), 못 가질 수도 있다(삼각 행렬).
6) 행렬 A의 eigenvalue가 양수이면 A는 positive definite matrix이고 극소점을 가지며, 음수면 negative definite matrix이고 극대점을 갖는다. Definite와 hessian, 극값에 대한 내용은 계속해서 나와 따로 정리했다.[Statistic] - Hessian 행렬과 Positive-Definite
Hessian 행렬과 Positive-Definite
Definite 정의 $f(x) = X^TAX = a_{11}x_1^2 + 2a_{12}x_1x_2 + \cdot \cdot +a_{nn}x_n^2, \ X\in \mathbb{R}^n$ 위와 같이, n개 변수를 갖는 quadratic form 함수 f(x)가 있을 때, 극점 x = 0을 제외한 모든 x..
hyunlee103.tistory.com
6. Singular value decomposition(특이값 분해)
SVD는 행렬을 singular vector와 singular value로 분해한다. 얻을 수 있는 정보는 고윳값 분해와 동일하지만, 정방행렬에만 적용 가능한 고윳값 분해를 모든 실수 행렬에 적용 가능하게 확장했다. 다음과 같이 분해하며, U, V는 orthogonal matrix, $\sum$는 singular value를 대각 원소로 갖는 대각 행렬이다.
$A = U\sum V^{T}$
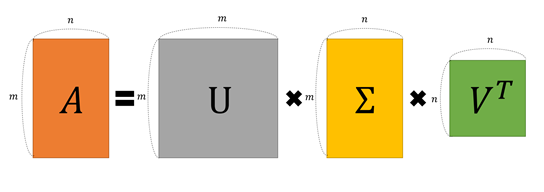
행렬 $A$의 singularvalue는 행렬 $A^{T}A$의 eigenvalue 제곱근과 같다.
$\sigma_A = \sqrt{\lambda_{A^{T}A}}$
SVD를 활용해 데이터 압축 및 복원할 수 있고, 비정방 행렬의 근사 역행렬(pseudoinverse)을 구할 수 있다.
7. Moore-Penrose Pseudoinverse
비정방 행렬(non-squre matrix)에서 SVD를 이용해 역행렬을 근사적으로 구하는 방법. 비정방행렬 A가 $UDV^{T}$로 svd 될 때, A의 pseudoinverse는 다음과 같이 정의한다.
$A^{+} = VD^{+}U^{T}$ , $D^{+}$는 0이 아닌 값을 역수 취한 D
8. Trace Operator
$Tr(A) = \sum_{i}^{}A_{i,j}$
Trace는 행렬 대각 원소의 합, transpose와 행렬곱에 대해 invarient 한 연산자. Tr(A)는 A의 eigenvalue들의 합과 같다.
9. Determinant
행렬을 실수 스칼라로 mapping 하는 함수, det(A)는 행렬 A의 모든 eigenvalue값을 곱한 것과 같다. det(A)의 절댓값은 주어진 행렬로 선형 변환했을 때 공간이 얼마나 확장, 축소되는지 나타낸다. det(A) = 0이면 적어도 하나의 차원에서 완전 축소되어 공간 부피가 0이 된다.
10. PCA(principle component analysis)
기하학적 접근
PCA는 인풋 데이터의 공분산 행렬에 대한 고윳값 분해로 구한 eigenvector에 원래 데이터를 projection 시켜 차원 축소 및 변수 생성 효과를 주는 분석 방법이다. 이때, 공분산 행렬의 eigenvector가 principal axes, 데이터 분산이 큰 축의 방향을 나타내고 대응되는 eigenvalue가 분산의 크기를 나타낸다. principle axes(eigenvector)에 원래 데이터를 projection 시킨 점이 principle component(PC)이다. 인풋 데이터(X)를 0으로 centering 하면 공분산 행렬은 $\frac{1}{n}X^{T}X$이고 대칭 행렬이다. 대칭 행렬의 eigenvector들은 서로 orthogonal 하므로 모든 principle axes들은 서로 orthogonal 하고 이는 통계학적으로 pc가 서로 독립인 변수로의 역할을 할 수 있음을 의미한다.
해석적 접근
n차원 인풋 데이터 x를 저차원의 c로 mapping 후 복원하는 과정으로 pca를 생각해볼 수 있다(오토인코더 구조와 동일).


질문 정리
1. eigenvector, eigenvalue 의미
-> 왜 Tr(A) = sum e-value
-> 왜 det(A) = product e-value
2. 입력 데이터 공분산행렬($X^TX$)의 eigenvector가 왜 데이터(X)의 분산이 큰 축의 방향을 나타내게 되는지
데이터 X를 임의의 단위 벡터 e에 projection 한 뒤, 그 분산을 구해보자.
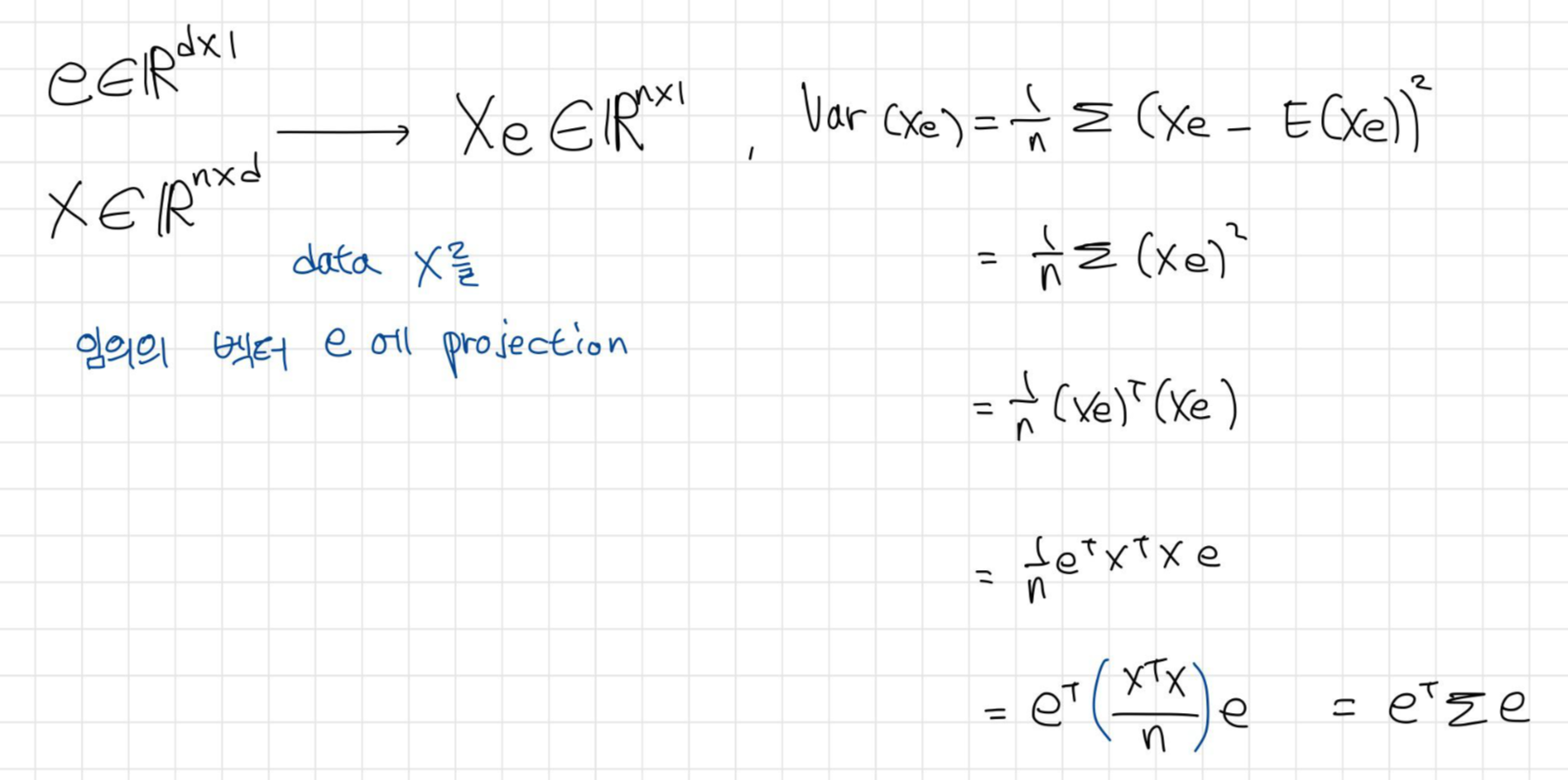
이때, 분산 $e^T\sum e$을 최대화 시키는 e를 찾는 최적화 문제로 생각하면,
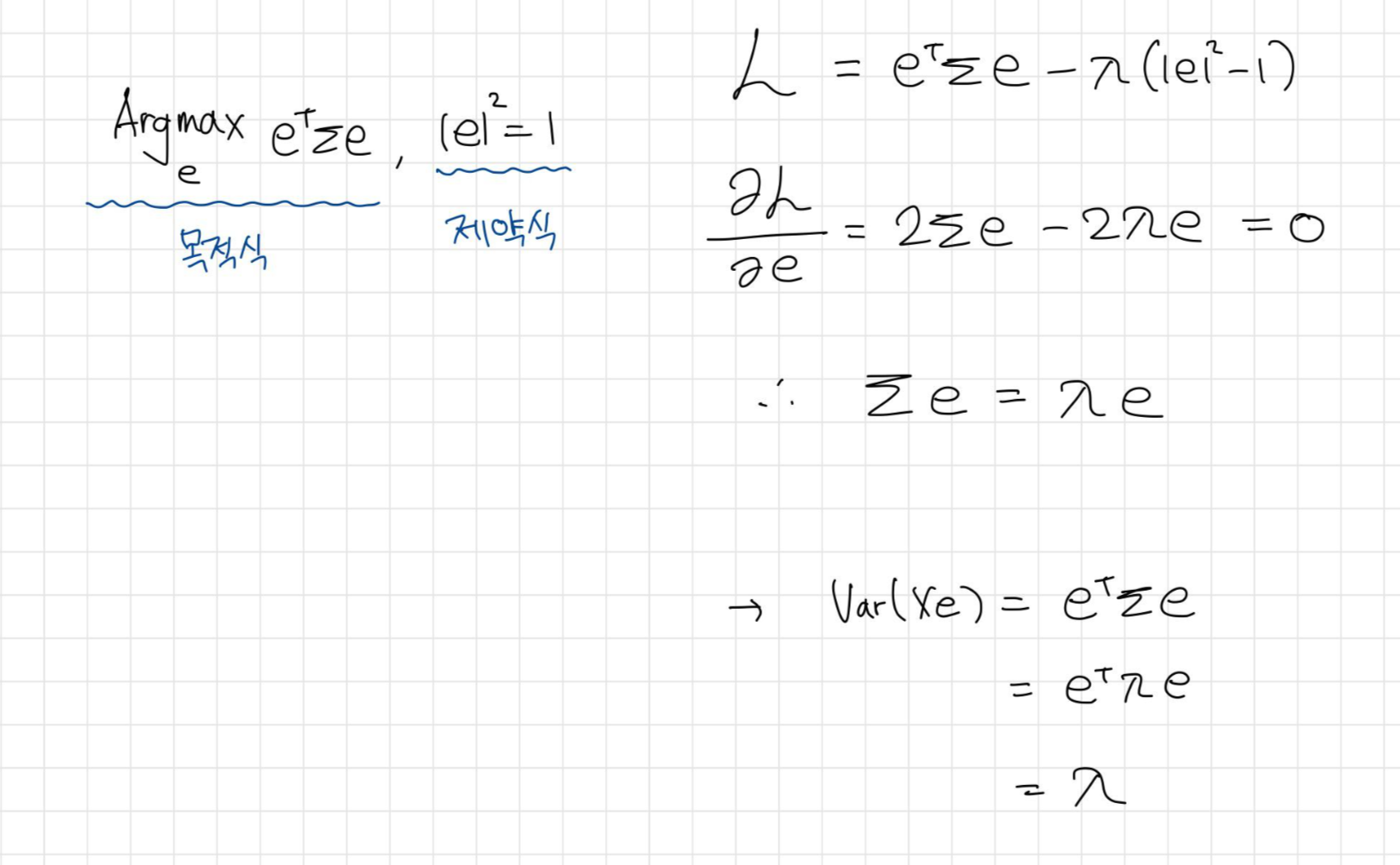
공분산 행렬 $\sum$의 eigenvector가 분산이 최대가 되는 벡터가 되고 그 크기는 eigenvalue가 됨을 알 수 있다.
'ML & DL' 카테고리의 다른 글
| [Deep learning] 8장 최적화 ① (1) | 2021.01.14 |
|---|---|
| [Deep learning] 3장 확률론과 정보 이론(probability, information theory) (0) | 2021.01.14 |
| [Deep learning] 6장 Deep Feedforward Network (0) | 2020.12.26 |
| [DL] Spectral Normalization (0) | 2020.06.04 |
| [Pytorch] Pix2Pix 구현하기 (6) | 2020.05.09 |

