처음 머신러닝을 공부할 때, 가장 어려웠던 부스팅 계열 알고리즘, 보아즈에서 발표를 하게 되면서 다시 한번 내용을 정리해두려고 한다. 학부생의 철없는 질문을 받아주신 건국대학교 권성훈 교수님과 이재병 연구원님께 감사의 말씀을 드린다.
INDEX
- Boosting이란?
- Basic Idea of Boosting
- AdaBoost
- GBM(Gradient Boost)
- XGBoost
- LightGBM
- Linear algebraic view of the Boosting
Boosting?
부스팅은 머신러닝 앙상블 기법 중 하나로 sequential한 weak learner들을 여러 개 결합하여 예측 혹은 분류 성능을 높이는 알고리즘이다. 사실 이 정의에 부스팅에 대한 핵심적인 개념이 다 들어있다. 하나씩 알아보자.
이건 교수님께 질문을 하며 알게 된 사실인데, 사실 부스팅은 Additive model 중 하나이다. Additive model은 비모수 회귀, 즉 함수 형태를 가정하지 않는 회귀모형을 의미한다. 부스팅이 이러한 Additive model에 속한다는 것은 결국은 회귀식 형태로 해석이 가능하다는 얘기인데, 조금 이따가 다뤄보도록 하겠다.
Basic Idea of Boosting
직역하면, 약한 학습기, 우리는 데이터를 통해 모델링을 하고 결국에는 새로운 데이터가 들어왔을 때, 예측이나 분류를 해주기 원한다. 따라서 모델은 학습 데이터에 너무 편향되면 안 된다(overfitting). 하나의 모델이 학습 데이터에 overfitting 되는 것을 막기 위해 약한 모델을 여러 개 결합시켜 그 결과를 종합한다는 게 기본적인 앙상블의 아이디어다.
부스팅은 여기에 sequential이 추가된다. 즉 연속적인 weak learner, 바로 직전 weak learner의 error를 반영한 현재 weak learner를 잡겠다는 아이디어이다. 이 아이디어는 GBM에서 loss를 계속 줄이는 방향으로 weak learner를 잡는다는 개념으로 확장된다.

위 그림을 보며 다시 정리해보면, 기존 학습 데이터에서 random sampling을 하고 1번 weak learner로 학습시킨다. 그 결과로 생긴 에러를 반영해 그 다음 데이터 샘플링과 2번 weak learner를 잡고 학습을 반복한다. 이 과정을 N번 하면 iteration N번 돌린 부스팅 모델이 되는 것이다. 부스팅 계열 모델은 AdaBoost, Gradient Boost(GBM), XGBoost, LightGBM, CatBoost 등이 있다. 순서대로 정리해보자.
AdaBoost

AdaBoost에서 weak learner는 stump라고 불리는 노드 2개짜리 tree model을 사용한다.
AdaBoost는 1997년에 개발된 최초의 부스팅 알고리즘이다. 직전 모델의 에러를 반영해 다음 모델에 weight를 주는 방식으로 학습한다. 이후 나온 GBM 계열 알고리즘이 더 성능이 뛰어나 요즘은 잘 쓰이지 않는 알고리즘이지만 그 아이디어는 알아두면 좋을 듯하다.다음의 과정을 통해 학습이 이루어진다.
1. 전체 데이터에서 random sampling
2. 모든 sample 데이터 가중치 초기화
3. 첫번째 weak learner 만들고 학습 후 결과에 따라(맞음 or 틀림) 각 데이터에 가중치(C)와 해당 weak learner의 모델 가중치(w) 출력
4. 3번에서 구한 데이터 가중치(C)로 데이터를 update
5. update된 데이터로 두 번째 weak learner를 만들고 학습한다. 3~5 과정을 N번 반복한다.
6. N번의 iteration 후, N개의 weak learner들에 각각 모델 가중치(w)를 줘서 최종 모델을 만든다.
수식으로 하나씩 뜯어보자!
1. 전체 데이터에서 random sampling
2. 가중치 초기화

3. 첫번째 weak leaner의 error 계산

4. 3번에서 구한 error를 바탕으로 데이터 가중치(c) 계산

5. 첫번째 weak learner 모델 가중치(w) 계산

6. 3~5 과정 N번 반복
7. 모델 가중치(x) Nomalize 후 최종 모델 도출


Gradient Boosting(GBM)
Sequential 한 weak learner들을 residual을 줄이는 방향으로 결합하여 object function과의 loss를 줄여나가는 아이디어. 여기서 정의되는 residual이 negative gradient와 같은 의미를 지니게 되므로 gradient 부스팅이라는 이름이 붙었다. 둘 사이의 관계를 살펴보자. loss function을 다음과 같이 정의하면,
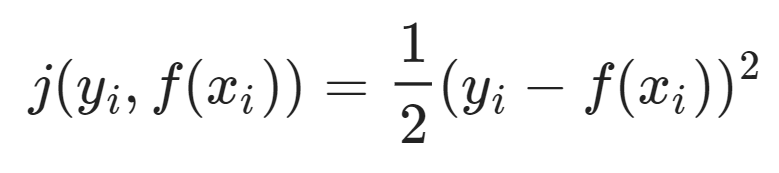
이 함수의 gradient는 다음과 같고,

앞에 - 를 붙혀주면,

위와 같고 residual(잔차)은 실제값과 예측값의 차이므로, 이는 residual을 나타내는 식과 같다. 따라서 loss function을 MSE로 정의했을 때, negative gradient = residual 이 성립하게 된다.

위에서 언급한 대로, GBM은 residual을 줄이는 방향으로 weak learner들을 결합해 나간다. 위 그림을 보면 tree1, 2, 3가 각각 weak learner가 되고 각 모델에서 실제값(점)과 예측값(파란선)의 차이(residual)를 다음 모델에서 fitting 시키고 있음을 알 수 있다. 수식으로 써보면,
F(x) = A(x) + E
F(x)가 object function, A(x)가 첫 번째 weak learner(tree1), E는 해당 모델에서의 error 즉 residual, 여기서 E(residual)를 다시 B(x)라는 weak learner로 fitting 시키면,
E = B(x) + E'
위 두 식을 합치면 다음과 같다
F(x) = A(x) + B(x) + E'
이 과정을 N번 반복한다 residual이 줄어드는 방향으로!!
F(x) = A(x) + B(x) + C(x) + ... + E''
GBM에서도 weak learner로는 tree model을 사용한다. Adaboost 보다는 복잡한 tree를 사용하는데, 최종 tree node가 8~32개 정도로 짜는 게 일반적이다(파이썬에서 hyperparameter로 튜닝이 가능하다).
GBM논문에 나온 수식으로 다시 살펴보자.

우선 Input data set과 미분 가능한 loss function을 정의한다. GBM에서 loss function은 주로 MSE , L1 loss, Logistic loss가 사용된다.
- Step 1에서 F0(x)로 초기 예측값을 준다.
- Step 2에서 학습을 진행하는데 1 ~ M 번 iteration을 돌린다.
(A) 위에서 정의한 loss를 미분해서 negative gradient = residual을 구한다.
(B) (A)에서 구한 residual을 target으로 하는 tree model(weak learner) 만들고 fitting 시킨다.
(C) loss를 최소로 하는 tree 결괏값을 출력한다. (이 과정은 생략되기도 한다)
(D) tree로 fitting 시켜서 구한 residual로 기존 예측값(F0(x))을 update 한다. 이때 gradient descent 알고리즘과 비슷하게 learning rate를 준다.
- Step 3 위 과정을 iteration 횟수만큼 반복 한 뒤, 최종 예측값을 출력한다.
XGBoost
GBM은 residaul을 줄이는 방향으로 weak learner를 결합해 강력한 성능을 자랑하지만, 해당 train data에 residual을 계속 줄이니까 overfitting 되기 쉽다는 문제점이 있다. 이를 해결하기 위해 XGBoost는 GBM에 regularization term을 추가한 알고리즘이다. 또한 다양한 loss function을 지원해 task에 따른 유연한 튜닝이 가능하다는 장점이 있다.
XGBoost = GBM + Regularization + 다양한 Loss function 지원
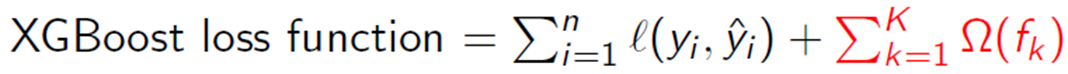
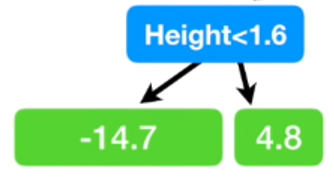
수식으로 보면 위와 같이 정의할 수 있다. 빨간색 부분이 regularization term이다. regularization term은 다음과 같이 정의된다. 여기서 T는 우리가 weak learner로 쓰는 tree의 최종 node의 개수, w는 최종 node의 score인데 loss function에 의해 학습되는 값이다.

따라서, XGboost의 regularization term은 tree 복잡도가 증가할수록 loss에 페널티를 주는 방식으로 overfitting을 막고 있음을 알 수 있다.
위에서 언급한 바와 같이, XGBoost는 다양한 loss function을 제공한다. 밑에 사이트에서 사용 가능한 loss function에 대해 확인 가능하다.
https://xgboost.readthedocs.io/en/latest/parameter.html < XGBoost documents
MSE와 같이 단순한 형태의 loss는 괜찮지만 다른 복잡한 loss들은 연산의 용이성을 위해 tayler expension을 통해 2차 근사 시킨 loss를 사용한다.

여기서 g는 1차 미분 함수(gradient) h는 2차 미분 함수(Hessian)가 된다. 이때 g와 h를 조정해주면 다양한 loss function을 사용할 수 있게 된다. 따라서 튜닝을 통해 새로운 loss를 정의하는 것도 가능하다. 이는 앞서 언급한 task에 따른 유연한 대처가 가능하게 해 줌을 의미한다.
Light GBM
부스팅 계열의 대부분 computational cost는 각 단계에서 weak learner인 best tree를 찾는데 쓰인다. 따라서 백만 개의 데이터를 XGBoost로 iteration=1000을 학습시킨 경우, 각 단계에서 tree를 fitting 시키기위해 백만개 데이터를 전부 scan 해야 한다. 해당 과정을 1000번 반복하니 computational cost가 너무 많이 들고 시간이 오래 걸린다. Light GBM은 이러한 높은 cost 문제를 histogram-based/GOSS/EFB 등의 알고리즘을 통해 tree를 구축하기 위한 scan 데이터 양을 줄임으로써 해결한다.
Linear algebraic view of the Boosting
서두에 언급했듯이, 부스팅은 Additive model 중 하나이다. Additive model은 비모수 회귀, 즉 함수 형태를 가정하지 않는 회귀모형을 의미한다. 부스팅이 이러한 Additive model에 속한다는 것은 결국은 회귀식 형태로 해석이 가능하다는 의미이다. 회귀분석을 해석하는 가장 직관적인 방법은 선형 대수적 접근이므로 이를 동일하게 부스팅에 적용해보고자 한다. 우선은 회귀분석 모델을 대수적으로 생각해보자.
b = A*x = A1*X1 + A2*X2 + ... + An*Xn + E

우리가 모르는 b라는 벡터를 예측하기 위한 C(A) ; colunm space A 공간 안에 있는 벡터들의 선형 결합이 회귀모형 식이다. 이를 풀기 위해 우리는 LSE를 정의하고 b 벡터와 가장 가까운 C(A) 공간 상의 벡터를 projection mapping을 통해 구할 수 있다. 이때 b를 만드는 A 벡터들이 C(A) 공간을 이루는 basis라면 이 회귀모형은 유일하고 자명한 해를 가지게 된다.
여기서 위에 회귀 모형식을 잘 살펴보면 우리가 GBM에서 정의한 weak learner의 결합과 비슷해 보인다. 즉, F(x) = A(x) + B(x) + C(x) + ... + E'' 에서 A(x), B(x), ... 등 이 회귀모형에서는 A1*x1, A2*x2, ....에 해당하는 것이다. 그렇다면 부스팅을 object function인 F(x) 공간을 정의하고 해당 공간 안에 basis를 잡고 F(x)를 지속적으로 fitting 시키면서 residual을 줄이는 것이라고 다시금 정의할 수 있다.
결국 부스팅에서 우리가 얘기했던 weak learner는 우리의 object function 공간에 basis이고, 이를 계속 움직이면서 sequential 하게 학습시키는 것이 부스팅 알고리즘이다. 회귀모형에서는 basis가 유클리디안 공간에서의 실수 벡터로 한정되었지만, vector space에서 vector는 함수로 정의되므로, 부스팅에서 함수로 정의되는(주로 tree 함수) weak learner들이 basis 역할을 할 수 있다.
Reference
- Introduction to statistical learning
- 권성훈 교수님, Ph. D. Professor. Department of Applied Statistics, Konkuk University.
- 이재병 연구원님
- https://www.slideshare.net/freepsw/boosting-bagging-vs-boosting
- A 1999 manuscript by Jerome Friedman that introduced Stochastic Gradient Boost: https://statweb.stanford.edu/~jhf/ftp/stobst.pdf
'ML & DL' 카테고리의 다른 글
| [논문] Deep Neural Networks for Acoustic Modeling in Speech Recognition(IEEE, 2012) (0) | 2020.03.06 |
|---|---|
| [강화학습] Lec.2 Markov decision process(MDP) (0) | 2020.02.02 |
| [강화학습] Lec.1 Introduction to Reinforcement learning (0) | 2020.01.19 |
| [NLP] Seq-to-Seq (0) | 2019.12.07 |
| [딥러닝]RNN과 LSTM (0) | 2019.11.18 |



