KAIST 문일철 교수님의 데이터 구조 및 분석 강의를 공부하고 정리한 내용입니다.
Repeating problem
Repeating problem이 있을 때, 문제를 나눠서 해결(divide and conquer). 해당 문제를 해결하는 함수를 recursive하게 사용한다. 즉, 함수 안에서 재귀 호출되는 함수는 divided된 동일한 문제를 해결하는 데 사용된다.
Factorial
$Factorial(n) = n \times Factorial(n-1) \quad if, \ n>0$
최대공약수(GCD)
Euclid's algorithm : GCD(A, B) = GCD(B, A mod B)
GCD(32, 24) = GCD(24, 8) = GCD(8, 0) <- 문제가 반복되며, 크기가 줄고 있다.
함수 반복, 파라미터 감소, 점화식과 유사
Recursion(재귀 호출)
함수안에 그 함수를 다시 호출하는 방식.
# pseude
def functionA(target):
...
functionA(target*)
...
if(escapeCondition):
return A모든 recursion은 escape condition이 있어야 한다! recursion의 예시로 피보나치 수열을 구현해보자.
def Fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
result = Fibonacci(n-1) + Fibonacci(n-2)
return resultFibonacci(4)를 실행하면, 실행 흐름은 다음과 같다.

F(4)가 가장 먼저 호출되고, n이 0, 1 아니므로 result에 F(3)이 호출되어 다시 함수 위로 올라간다. F(n-2)는 호출되지도 목한다. 그다음 F(2), F(1) 이 차례로 호출되고 F(1)에서 return이 발생하므로 재귀를 빠져나와 F(n-2) (= F(0))를 호출한다.
Stackframe
function call history를 저장하는 stack. 함수가 호출될 때 push 되고 return 될 때 pop 된다. R.A(return address)와 함수가 호출될 때 파라미터를 저장한다. F(1)이 return되면서 pop되어 stackframe에서 빠지고 그 다음 호출된 F(0)이 stack에 push 된다.
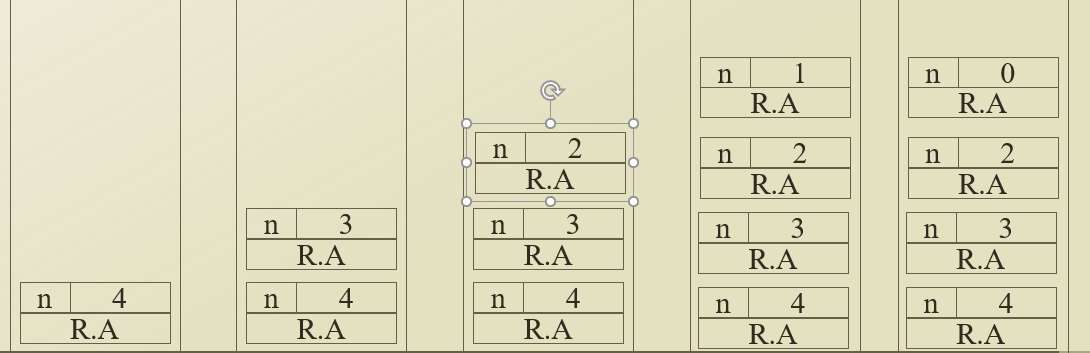
Merge sort
주어진 list를 반으로 decompose해서 single value 까지 내려간뒤, 대소를 비교해 sort해서 합친다(aggregation).

def Mergesort(lstTosort):
if len(lstTosort) == 1:
return lstTosort
sub_lstTosort1 = []
sub_lstTosort2 = []
for itr in range(len(lstTosort)):
if len(lstTosort)/2 > itr:
sub_lstTosort1.append(lstTosort[itr])
else:
sub_lstTosort2.append(lstTosort[itr])
sub_lstTosort1 = Mergesort(sub_lstTosort1)
sub_lstTosort2 = Mergesort(sub_lstTosort2)
idx1 = 0
idx2 = 0
for itr in range(len(lstTosort)):
if idx1 == len(sub_lstTosort1):
lstTosort[itr] = sub_lstTosort2[idx2]
idx2 += 1
elif idx2 == len(sub_lstTosort2):
lstTosort[itr] = sub_lstTosort1[idx1]
idx1 += 1
elif sub_lstTosort1[idx1] > sub_lstTosort2[idx2]:
lstTosort[itr] = sub_lstTosort2[idx2]
idx2 += 1
else:
lstTosort[itr] = sub_lstTosort1[idx1]
idx1 += 1
return lstTosort
Problems in Recursions
함수 호출이 너무 많고, 심지어 동일한 파라미터를 갖는 함수 호출이 중복되어 비효율적이다. 이를 해결하기 위해, 호출된 함수의 정보를 저장하는 방법을 통한 Dynamic programing을 사용한다.
Dynaminc Programming 1 (memoization)
sub-probelms이 중복되는 문제를 해결하기 위한 general algorithm. 작은 문제부터 해결해가며 각 return 값을 저장을 해둔 뒤, 이를 이용해서 점점 큰 문제를 해결해가는 방법이다.
DP는 앞서 살펴 본 Recursion과 구조적으로 반대 flow를 갖는다.

recursion은 top-down 으로 task의 맨 위, 즉 F(4) 부터 함수를 호출해가며 문제를 해결한다. 반면 DP는 가장 작은 sub instance인 F(0) 부터 그 결과를 memoization에 저장해가며 bottom-up 으로 문제를 해결한다. recusion의 overlapped functin call이 많다면 DP를 통해 메모리 효율을 높이는게 좋다.
피보나치 DP
def FibonacciDP(n):
dic = {}
dic[0] = 0
dic[1] = 1
for itr in range(2, n+1):
dic[itr] = dic[itr-1] + dic[itr-2]
return dic[n]recursion과 다르게 매 0, 1 결과값으로 그 다음 스텝 값을 계속 저장해간다. 여기서 dic이 memoization table이 된다.
Assembly Line Scheduling
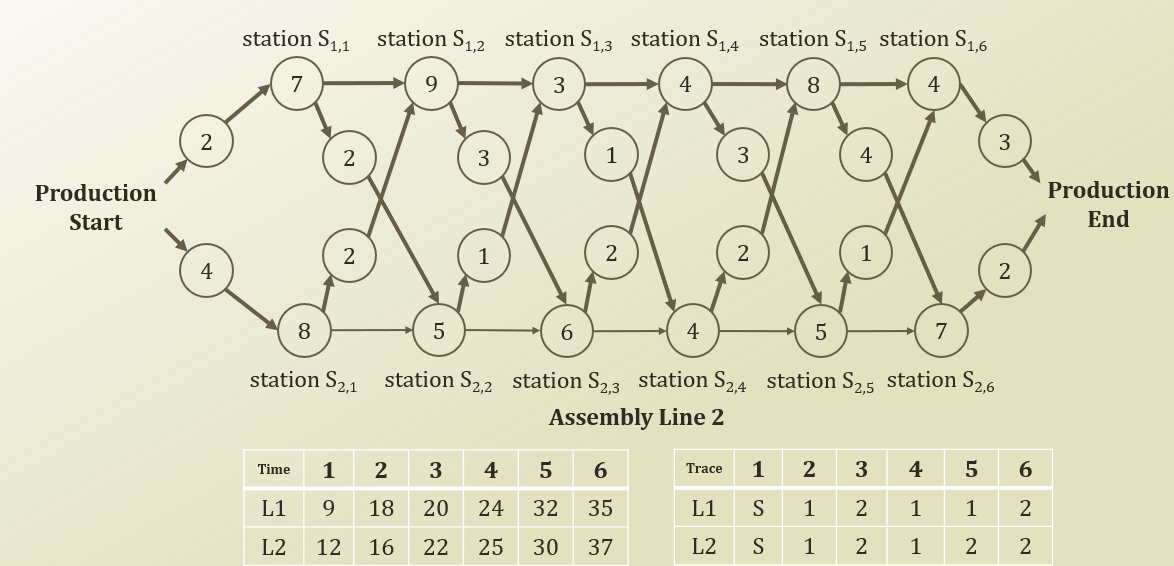
memoization table로 각 station의 min time을 저장하고, trace table에 최적 path 이전 station을 저장한다. 이를 통해 최적 path를 problem groth를 통한 DP로 구할 수 있게 된다.
Summarize
recursion은 파라미터를 줄이며 함수안에서 함수를 재귀 호출한다.
DP는 이전 함수 호출 결과를 다음에 사용하기위해 저장한다.
DP와 recursion은 flow가 반대이고, 동일한 task를 두 가지 방법으로 모두 해결할 수 있다.
reference
KAIST 문일철 교수님, Linear Structure and Dynamic Programming
https://www.edwith.org/datastructure-2019s/joinLectures/21992
'Programming' 카테고리의 다른 글
| 객체지향 프로그래밍(1) class, method, instance (0) | 2020.12.29 |
|---|---|
| [알고리즘] 하노이 탑(recursion) (0) | 2020.06.22 |
| 파이참(Pycharm)에서 데이터 프레임 확인하기 (0) | 2020.05.04 |
| 파이참(Pycharm)에서 주피터처럼 라인 실행하기 (1) | 2020.05.04 |
| Anaconda + 파이참(Pycharm), 가상환경 구축하고 연동하기 (7) | 2020.05.02 |
