추천 시스템에서 사용되는 Factorization Machine과 그 발전 모델인 Field Award Factorization Machine(FFM)에 대해 공부하고 정리한 글입니다.
original paper : https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf
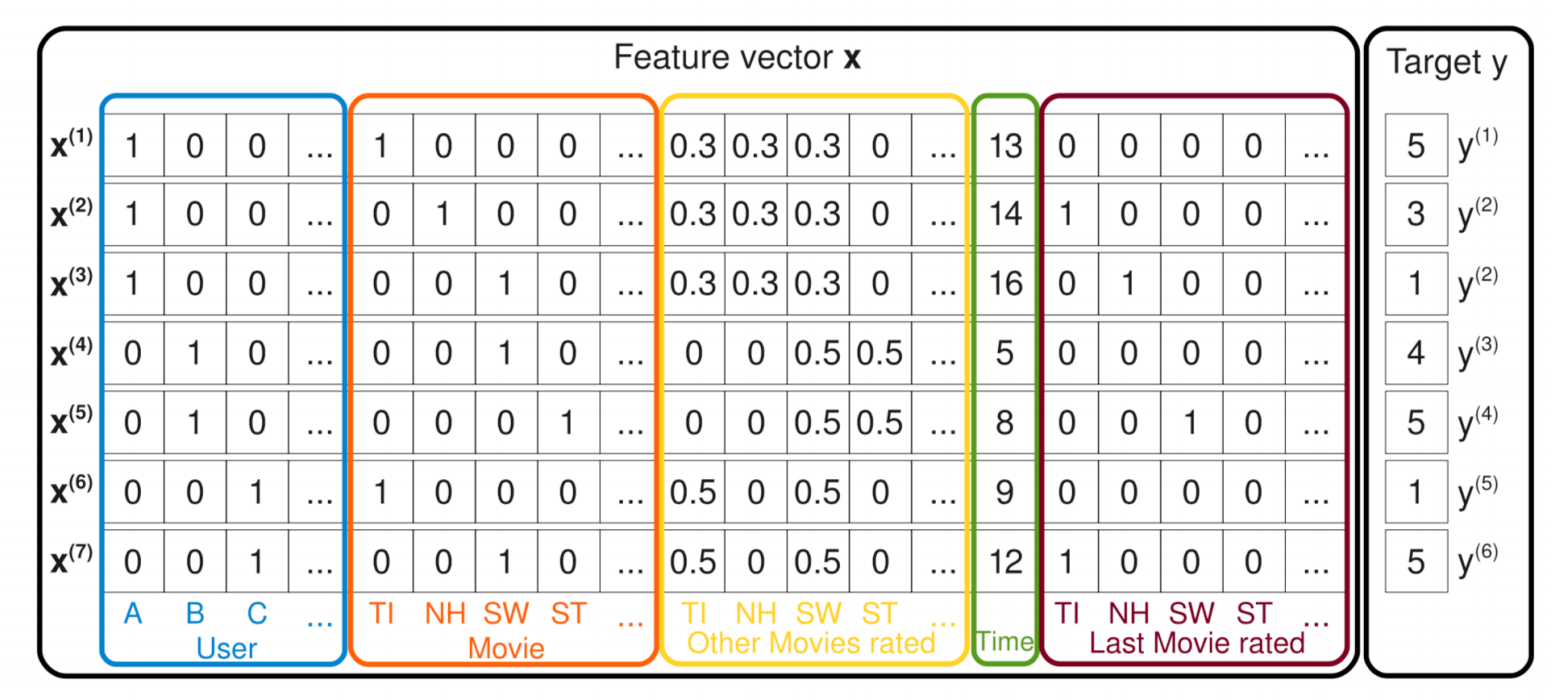
추천 시스템에서 주로 사용하는 데이터는 위와 같다. categorical type 변수가 많고 따라서 one-hot-encoding된 데이터 값이 많다. one-hot vector 특성상 데이터 차원이 크고 상당히 sparse 하다.
Linear model
FM에 대한 논의를 선형 회귀식에서 시작해보자. 위 데이터를 일반적인 선형 회귀문제라고 생각하고 모든 변수를 X 예측하고자 하는 값을 y로 두면, LM 수식은 다음과 같이 정의 된다.
$\widehat{y} = w_0 + \sum_{i=1}^{n}w_ix_i$
하지만 높은 차원의 데이터, 높은 sparsity, 무시된 변수 간 interaction 등 LM은 여러 한계가 있다. 이를 보완하기 위해 polynomial regression을 고려하거나, 비선형 모델인 SVM, NN 등을 사용할 수 있다. 각 변수 간 interaction을 고려한 polynomial model(2)의 수식은 다음과 같다.
$\widehat{y} = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{ij}x_ix_j$
이렇게 모델링을 하면, LM의 여러 한계를 극복할 수 있지만, paremeter 수의 증가로 연산 복잡도가 증가하게 된다. Factorization machines은 feature interaction vector를 저차원으로 factorize해서 이를 해결한다. 이게 무슨 말인지 알아보자.
Factorization model(FM)
$\widehat{y} = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}(\vec{v_i}\cdot \vec{v_j})x_ix_j$
FM 수식은 위와 같다. 앞서 살펴 본 poly model에서 interaction weight인 $w_{ij}$ 가 두 벡터($V_i, V_j$)의 내적으로 분해(factorize)되었다. 즉 두 변수의 interaction을 하나의 값인, $w_{ij}$으로 표현하지 않고 k차원으로 factorizing 된 두 벡터($V_i, V_j$)의 내적으로 표현한다. 이 두 벡터는 변수 간 interaction의 latent vector이며 기존 변수의 정보를 k 차원으로 확장시켜 표현한다. Sparse 환경에서 변수들은 서로 독립성이 강해 interaction을 포착하기 어려운데, 각 변수 정보를 latent vector로 표현함으로써 latent space 내에서 독립성을 깨고 interaction을 보다 더 잘 잡아낼 수 있다. 다음의 예시를 보자.

User B, C ($X_B, X_C$)는 겹치는 값이 하나도 없으므로 interaction이 0이다. 하지만 해당 두 변수의 latent vector를 이용하면 숨겨진 interaction을 구할 수 있다. $V_{sw}와 두 user의 latent vector와의 내적은 유사하다. 이를 이용해 두 유저 latent vector가 유사도(interaction)가 높음을 알 수 있다.
또한, 다음과 같은 전개를 통해 연산 복잡도를 줄일 수 있다.
$\begin{aligned}
\sum_{i=1}^{n}\sum_{j=i+1}^{n}(\vec{v}_i \cdot \vec{v}_j)x_ix_j &= \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}(\vec{v}_i \cdot \vec{v}_j)x_ix_j - \frac{1}{2}\sum_{i=1}^{n}(\vec{v}_i \cdot \vec{v}_i)x_ix_i \\
&= \frac{1}{2}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{j,f}x_ix_j - \sum_{i=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{i,f}x_ix_i\right) \\
&= \frac{1}{2}\sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n}v_{i,f}x_i\right)\left(\sum_{j=1}^{n}v_{j,f}x_j\right)-\sum_{i=1}^{n}v_{i,f}^2x_i^2\right) \\
&= \frac{1}{2}\sum_{f=1}^{k}\left( \left( \sum_{i=1}^{n}v_{i,f}x_i \right)^2 - \sum_{i=1}^{n}v_{i,f}^2x_i^2 \right)
\end{aligned}$
k는 충분히 n에 가까워야 데이터 손실이 적을 것이고, 작을 수록 연산 효율성이 좋아지므로 trade-off 관계를 적절히 이용하여 최적의 k를 찾는 것도 중요하다.
FFM(Field Award Factorization Machine)
FFM은 FM에서 발전한 모델로, 변수를 여러 field로 분리한 뒤, 각 field latent space로 interaction을 분해(factorize)한다.

편의를 위해 데이터가 1개 있는 위와 같은 set을 보자. 여기서 P, A, G는 각 변수의 field가 된다. FMM의 아이디어는 field에 따라 서로 다른 field에 대해 주는 interaction이 다를 것이므로, 이를 각각 모델링하는 것이다. 예를 들어 위 데이터에 대한 FM interaction latent space는 모든 변수에 대해 다음과 같다.
$V_{ESPN}\cdot V_{Nike}+V_{ESPN}\cdot V_{Male}+V_{Nike}\cdot V_{Male}$
하지만, FFM의 경우 다음과 같이 (P x A) space, (P x G) space, (A x G) space로 각각 분리 된 latent space 위에 interaction vector V가 표현된다.
$V_{ESPN,A}\cdot V_{Nike,P}+V_{ESPN,G}\cdot V_{Male,P}+V_{Nike,G}\cdot V_{Male,A}$
즉 latent vector V가 상호작용하는 field에 특정되어 정의된다. 따라서 기존의 k차원 V는 field 차원 만큼 확장하게 된다. 여기선 field가 3개니까, k x 3. 다음 그림은 LM, FM, FFM의 latent vector를 보여준다.

Reference

