스탠퍼드 머신러닝 3주차인 Logistic Regression 강의를 듣는데, 여기서 사용되는 Cost function이 MLE 기반으로 유도된다는 얘기를 듣고 아예 MLE 기반의 estimator들과 cross-entropy까지 한꺼번에 공부해서 정리해야겠다는 생각이 들었다. 학교 수리통계학 시간에 배운 MLE 개념과 베이지안 접근(Baysian approach)이 머신러닝에서는 어떤식으로 확장되어 사용되는지 궁금했다.
우리가 그냥 가져다 쓰던 logistic 함수 cross-entropy 모두 MLE와 베이지안 관점에서 통계적으로 유도된 함수들이었다. 수리적으로 엄밀하고, 또 왜 MLE가 머신러닝과 딥러닝에서 좋은 Estimator로 쓰이는지 깊게 생각해보게 되었다.
이 글은 PC 환경에 최적화되어 작성되었습니다!
▶분류(Classification)문제에 대한 접근
이전까지 다루던 회귀 문제에서 벗어나, 분류 문제를 대할 때 단순 회귀로는 적절한 결과를 도출 할 수 없음을 알 수 있다. 따라서 도입된 방법이 logistic regression이다. 어떤 종양이 양성인지 음성인지, 이메일이 스팸인지 아닌지 와 같은 binary classfication(이진 분류)부터 수능 등급을 예측해 분류하는 multinomial classification까지 logistic regression은 다양하게 적용할 수 있는 알고리즘 이다.

▶ 로지스틱 함수(Logistic Function) : 2-Class Classification
대다수의 자연, 사회 현상에서의 특정 변수에 대한 확률 값은 선형이 아닌 S-커브 형태를 띄는 경우가 많다. 일례로 경제 자료의 경우 한계 효용, 수확 체감등의 원리로 S-커브 형태를 띄는 것에 대한 이론을 정립해 놓기도 했다. 이진분류(binary classification)에 쓰이는 logistic 함수도 S-커브 형태를 따르는데 이를 bayes 정리에 기반에 유도해 보겠다.
Bayes Thorem

위 식에서 X는 Data, Y는 우리가 분류할 class라고 생각하자. 좌변은 사후 확률(posterior), P(X | Y)는 Likelihood, P(Y)는 Prior 그리고 P(X)는 Evidence라고 부른다.
Prior은 class들의 분포에 대한 사전 지식을 의미하고, P(X | Y)는 각 class에 속해 있는 Data의 확률 분포, 그리고 사후 확률 P(Y | X)는 새로운 데이터 X가 들어 왔을 때, Y 즉 class의 확률 분포로, 이 확률을 통해 어떤 class에 속할 지를 정할 수 있다. 다시 말해 새로운 데이터 X가 들어왔을 때 어떤 class에 속할 확률을 반환한다. 확률이므로 0과 1사이의 값을 가지고 확률 분포의 성질을 가진다.
Logistic Function
우리는 이진 분류(binary classification)에 대해 다루고 있으므로 위에서 정의한 식에서 Y(class)가 Y1, Y2 두개의 class가 있다고 하고 각각의 posterior을 전개해보자. posterior은 우리가 예측한 모델이 된다.

식을 보면, 분포가 P(X)로 동일하므로 결국 각 Class에 대한 사후 확률은 Likelihood와 Prior의 곱에 비례함을 알 수 있다. k번째 class에 대한 Likelihood와 Prior의 곱을 다음과 같이 ak로 정의하자.
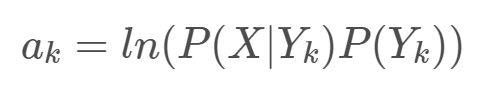
여기서 ak를 로그를 취해 정의하는 이유는 MLE를 계산할 때 Log likelihood를 이용하는 이유와 동일하다. Log 스케일링을 함으로써, 곱 연산이 덧셈으로 바뀌어 계산이 용이해지고, 정규분포나 포아송 같은 지수족일 경우 다시 한 번 계산이 쉬워진다. 무엇보다도 log는 단조 증가 함수(monotone-increasing function)이므로 함수의 극점을 변화시키지 않는다. 즉 최적화 기점을 유지시켜 준다는 것이다.
이제 다시 Class 1의 posterior을 추정해보면
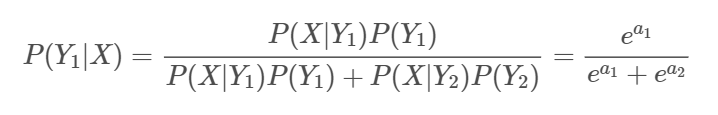
분모, 분자를 분자로 각각 나눠주면,
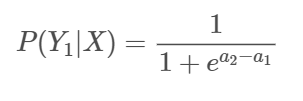
exp안에 식을 a로 재정의 하면(Log Odds)

최종적으로 우리가 알고있는 Logistic function(Sigmoid function)이 된다.

Naive Bayes 기반의 분류 문제에서 Likelihood는 정규분포로, Prior은 class 분포에 대한 사전 믿음이므로, Bernoulli 분포로 두면 적당하다. Likelihood를 정규분포로 가정하는 이유는 한 Class 내에서의 data의 분포가 정규 분포가 좋기 때문이다.
위에 정의한 a(Log Odds)에 이러한 분포들이 들어가게 되면 Naive Bayes 분류기가 되며, 이는 대표적인 Generative Model이다.
여기서, Likelihood와 Prior의 확률 분포에 기반하지 않고 바로 Posterior, P(Y | X)를 직접적으로 추정하는 모델이 Discriminative Model 중 하나인 Logistic Regression이 된다.

그럼 Discriminative Model 에서, a에 wx를 쓰는 것은 왜 그럴까? (세타 대신 w로 표기했습니다.)
만약, Class의 분포가 정규분포이고, 공분산 행렬(Covariance Matrix)을 공유할 경우,

위에 식과 같이, a를 W들의 선형 결합으로 나타 낼 수 있게 된다.
▶ Logistic Regression의 결정경계(dicision boundary)
위에서 우리는 Logistic function에 대해 정의했다. 이 함수에 data x를 넣으면 범주 1에 속할 확률을 반환해 준다. 하지만 이 확률을 이용해 결국 y를 0과 1에 mapping 시켜야 되기 때문에 이를 구분 짓는 경계가 필요하다. 여기서 이 경계(dicision boundary)는 우리의 추정값인 h(x)에 전적으로 의존하며 실제 train data와는 무관하다.

위와 같이 우리의 가설을 정의했을 때, logistic 함수의 형태는 다음과 같이 나오게 된다.

그래프에서 Z, 즉 WX가 양수인 영역에서 y를 1로 음수인 영역에서 y를 0으로 mapping 시키자. 이때 나누는 기준인 WX = 0 (하이퍼 플레인)이 Dicision boundary가 된다. 입력 벡터가 2차원인 경우에 다음과 같이 시각화할 수 있다.
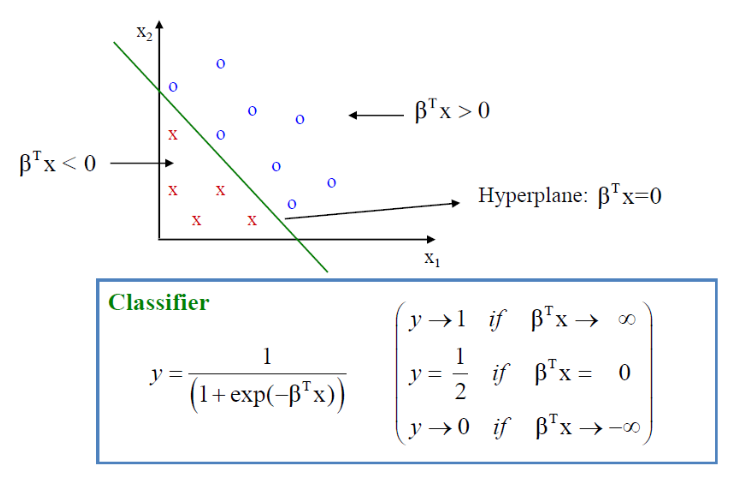
만약 Dicision boundary가 비선형인 경우에는 Z, 즉 WX가 polynomial 식으로 표현되야 한다. 예를 들어 다음과 같은 데이터를 분류해야 한다고 해보자.

Dicision boundary가 원의 형태로 나타나므로 WX에 2차항을 추가해 polynomial term으로 구성해주면 비선형인 경우의 dicision boundary도 구할 수 있다.
▶ Logistioc Regression의 Cost function(Cross-entropy)과 학습
로지스틱 회귀 모델에서는 계수 W를 추정하기 위해서 MLE(Maximum Likelihood Estimation) 개념을 사용한다. 로지스틱 회귀의 Y는 이진 분류(0 or 1)이므로, 베르누이 시행을 전제로 하는 모델이다.
베르누이 분포의 pmf는 다음과 같다.

이에 대한, Likelihood function은 다음과 같다.

여기서, p는 y가 1이 나올 확률이다. 즉 우리가 정의한 logistic function의 output과 동일하다. 따라서 p에 로지스틱 함수를 대입하면 로지스틱 함수에 대한 Likelihood를 다음과 같이 구할 수 있다.
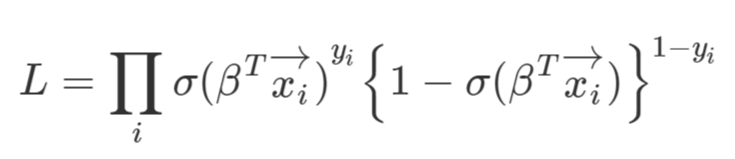
우리는 MLE를 사용할 것이므로, Log likelihood를 구해준다(log scaling의 이유에 대해선 위에서 언급했다)

따라서, 이 Log likelihood를 Maximize하는 B를 찾으면 되고 여기에 음수를 달면

우리가 구하려는 로지스틱 회귀의 Cost function이 나오게 된다. 기본적으로 Gradient descent를 통해 학습을 하므로 단순히 Maximize 문제를 Minimize로 바꾼 것이다.
즉, Negative Log Likelihood = (binary) Cross Entropy = Logistic regression cost function
자 그럼, 이 Cost function 즉 로지스틱 회귀의 Cross entropy가 Convex 한지를 증명해보자. 어떤 함수의 Convex를 증명하기 위해선 2차 미분값이 > 0 증명하면 된다.
우선 우리의 Cost function을 Tayler 전개를 통해 2차 함수로 근사시킨다.

다변수 함수에서 H는 Matrix 형태가 되고, 이를 Hessian이라고 정의한다. 이 Hessian matrix가 Positive Definite 하면, Convex가 보장되는데, 다음과 같을 때 p.d 하다고 한다.

다시 우리의 Cost function으로 돌아와서 Hessian * XtX를 구해보면 다음과 같게 되는데,

X는 벡터인데, 자기 자신과의 내적이므로 항상 양수이고, y는 Logistic function의 output으로 0과 1사이의 값을 가지는 확률이므로 항상 양수, 즉 Positve Definite가 되어 Convex를 보장하게 된다.
위 Cost Function은 W에 대해 비선형이기 때문에 선형 회귀와 같이 명시적인 해가 존재하지 않는다. 따라서 SGD(stochastic Gradient Descnet) 같은 반복적인 점진적인 방식으로 최적 해를 구하게 된다.
최종 Cost function을 다시 정의해보면, 다음과 같다.
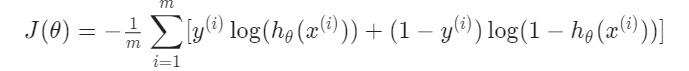
SGD를 위해 Vectorize 해주면,
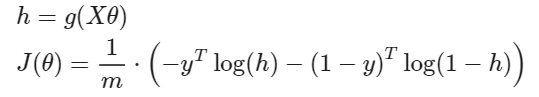
위 식을 Gradient descent 시키면,
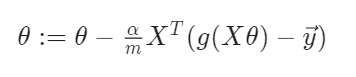
위와 같이 세타(W or B)를 학습할 수 있게 된다.
▶ 다항로지스틱 회귀(Softmax Function) : K - Class Classification
그러면 이진분류(Binary classification)이 아니고 다항분류의 경우에는 어떻게 될까?
일단 위에 정의한 로지스틱 함수를 이용해 K개의 Class가 있을 때 특정 Class로 분류 될 확률을 구해보자.
우선, Class가 2개인 binary 문제에서 Class 1에 대한 posterior 추정 확률은 다음과 같았다.

이를 K개의 Class 중 Class 1에 대한 posterior 추정으로 확장하면, Bayes 정리에 의해
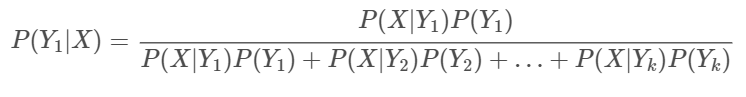
다시 위 식을 Likelihood와 Prior의 곱으로 표현한 ak 식으로 표현하면, 다음과 같다.

결국, 이것이 Softmax function이 되고, 로지스틱 함수와 동일하게 Likelihood와 Prior을 고려하지 않은 ak를 구해서 Fitting 시키면,

Discriminant 모델 중 하나인 Softmax Regression이 되고, Data X가 주어졌을 때, 전체 K개의 Class 중 Class1로 분류 될 확률값을 반환 한다.
▶ Cross entropy 와 Negative log-likelihood
P(x)를 우리가 가진 데이터의 분포 P(Y | X), Q(x)를 모델이 추정한 결과의 분포 P(Y | X;세타) 라고 할 때, 실제 데이터의 분포인 P(x)와 모델이 추정한 분포 Q(x)의 차이인 Cross- entropy는 다음과 같이 정의 된다.
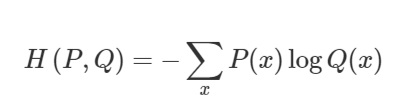
위 식은 파라미터 세타 하에서 Negative log-likelihood(logQ(x))의 기대값으로 해석가능하고 다음과 같이 표현이 된다.

따라서, Cross-entropy를 최소화하는 것은 실제 데이터의 분포와 모델이 예측한 결과의 분포의 차이를 최소화 하는 것이고, 이는 Log-Likelihood의 기대값이 최대인 세타를 찾는 것과 같다. 이 때문에 Negative log-likelihood가 머신러닝 모델의 Cost functuon이 되는 것이다.
▶ 왜 Negative log-likelihood?
앞서 살펴본 바와 같이, 머신러닝에서는 종종 Cost Function을 negative log-likelihood로 사용한다. 왜 MLE 기반 Cost function이 좋은지 알아보자.
1. 만드려는 모델에 다양한 확률 분포를 가정할 수 있게 돼 유연한 대응 가능
Negative log-likelihood로 cost function을 정의하면 이는 두 확률 분포의 차이인 크로스 엔트로피가 되고, 크로스 엔트로피는 대상 확률 분포의 종류를 특정하지 않기 때문이다.
2. Backpropa 시에 Gradient가 죽는 문제는 어느정도 해결 가능
3. MLE에 기반에 추정한 모수는 일치성(consistency)과 효율성(efficiency)를 만족하는 Estimator가 된다.
일치성을 만족하면 Data의 크기가 커질 수록 실제 값에 수렴하는 특성을 가지게 된다.

또한, MLE 크래머-라오 하한 정리에 의해 일치 추정량 중 가장 분산이 작은 estimator가 되고 이를 효율성을 만족하는 추정량이라고 한다. 따라서 MLE는 데이터의 크기가 매우 큰 머신러닝과 딥러닝에서 좋은 추정량이 된다.
다음은 크래머-라오 하한 정리를 통해 추정량의 분산의 하한을 결정하는 수식이다.

나름 정리한다고 열심히 했는데 분명, 빠진 개념이나 부족한 부분이 많이 있을거에요. 지속적으로 다시 쓸 생각이고 내용과 관련해서 댓글로 질문이나 의견을 제시해주시면 정말 정말 감사할 것 같습니다 :)
logistic은 항상 분류 문제의 기본이 되며, 설명 가능하다는 큰 장점이 있어 산업 단계에서 많이 쓰인다. 또한 통계적으로 철저하게 검증되어 발전된 이론으로 data에 영향을 크게 받지 않기에 강력한 방법이다.
binary logistic regression에서는 내가 예측하고자 하는 값을 1로 두고 진행한다.
Reference
1. ratsgo 블로그 https://ratsgo.github.io/statistics/2017/09/23/MLE/
2. Teaoh Kim's 블로그 https://taeoh-kim.github.io/
3. 위키피디아 https://en.wikipedia.org/wiki/Cram%C3%A9r%E2%80%93Rao_bound
4. Introduction to Mathematical Statistics (7E, Robert V. Hogg)
5. 유규상 교수님(Kyusang Yu, PhD. Professor. Department of Applied Statistics. Konkuk University)
'Statistic' 카테고리의 다른 글
| [정보이론] KL-divergence의 비대칭성과 Cross Entropy (0) | 2021.02.04 |
|---|---|
| Hessian 행렬의 고윳값과 definite (0) | 2021.01.15 |
| 독립과 직교(orthogonal) (2) | 2021.01.09 |
| [TIL] Softmax에서 왜 e를 쓸까 (4) | 2020.12.10 |



