Entropy
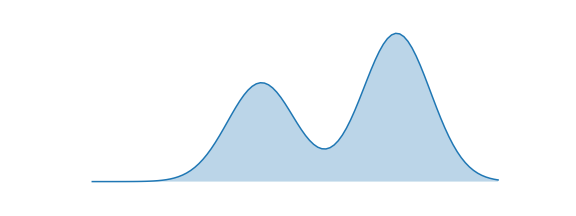
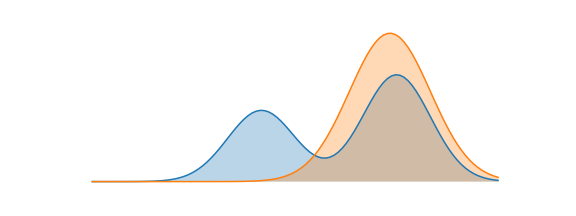
엔트로피는 특정 확률분포가 갖는 불확실성, 무질서 정도를 정보량의 기댓값으로 수치화한 값이다. 엔트로피가 큰 분포는 분산이 큰 정규분포, 엔트로피가 작은 분포는 분산이 작아 특정 영역에 확률값들이 모여 있는 분포다. 아래의 녹색 strong prior가 엔트로피가 작은 분포, 파란색 weak prior가 엔트로피가 큰 분포이다.

$X$ : event point
$P(X=x)$ : event 확률
$-logP(X)$ : X의 정보량(self-information)
$E_{X\sim P} [-logP(X)]$ : 확률분포 P(X)의 entropy(정보량 기댓값)
KL-divergence
KL-divergence는 확률분포간 정보량 차이로 확률분포 P(x)와 Q(x)의 차이를 측정한다. 이를 P 분포를 추정하는데 Q 분포가 얼마나 적합한지로 해석할 수 있다. 확률분포 P, Q가 같은 domain x를 갖는 경우에 KL-divergence 수식은 다음과 같다.

Properties
- KL divergence는 symmetric 하지 않다. 즉, $D_{KL}(P||Q) != D_{KL}(Q||P)$ 이고 distance metric 으로 역할을 하지 못한다.
- KL divergence는 $[0, \infty ]$ 범위의 값을 갖고, $D_{KL}(P||Q) = 0$ 이면 반대도 0이고, P, Q는 동일한 분포다.
- KL divergence가 유한한 값을 갖기 위해선 P, Q의 support가 겹치는 영역이 있어야 한다.
cross entropy
다음과 같이 KL-divergence 식을 변형하면 확률분포 P, Q 사이의 cross-entropy가 유도된다.
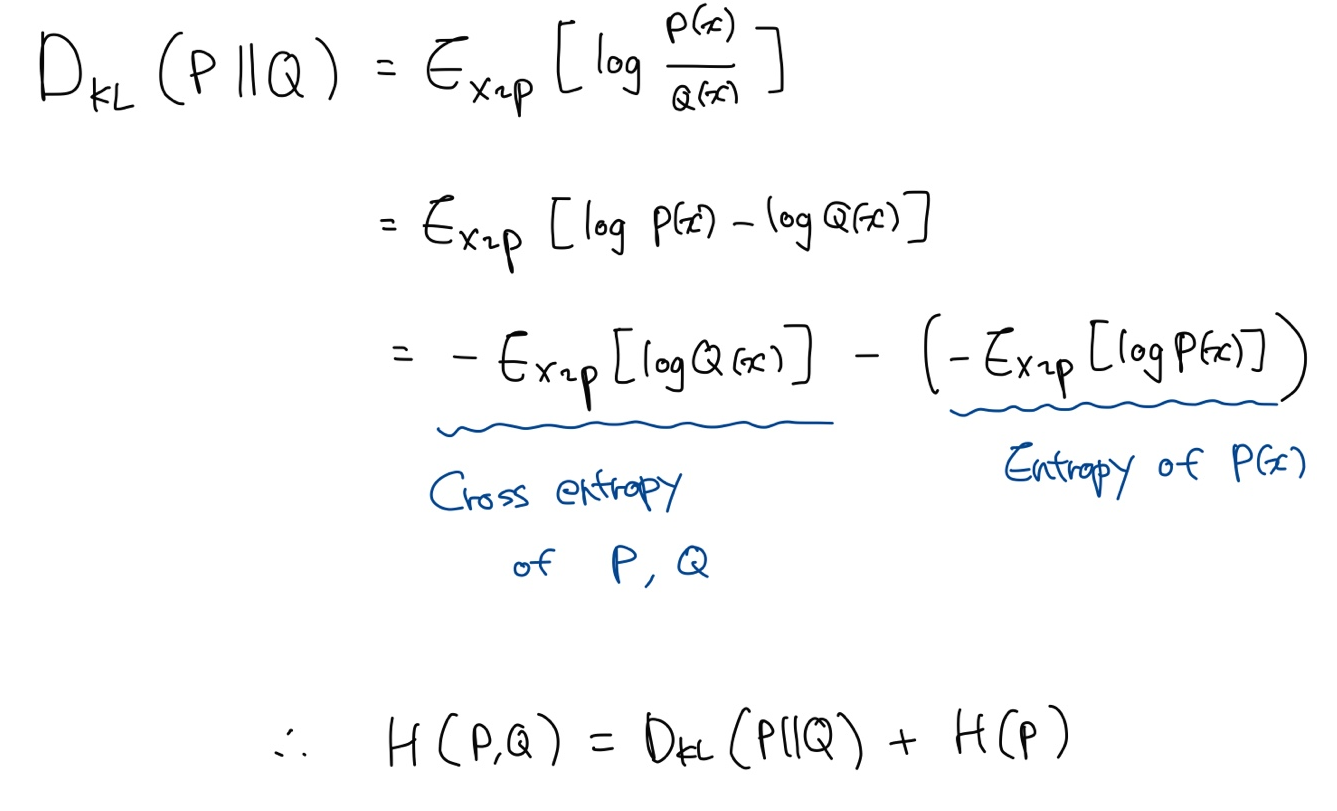
즉, cross entropy는 KL에 P의 entropy를 더한 값이다. 이때 $H(P)$는 Q와 무관한 term이므로, Q에 대해 KL을 최소화하는 것과 cross entropy를 최소화하는 것은 같다.
KL-divergence optimization
정답 분포 $P(x)$를 $Q_\theta(x)$로 근사하는 $\theta$를 추정하는 과정을 다음과 같은 최적화 과정으로 수식화 할 수 있다.
$\arg min_\theta D_{KL}(P||Q_\theta)$
$\arg min_\theta D_{KL}(Q_\theta ||P)$
근데, KL-divergence는 비대칭이라 두 목적식이 달라, 두 최적화 식이 다른 방향으로 추정과 분포 근사가 이뤄진다. P(x)를 아래와 같은 bimodal 분포로, Q(x)를 정규분포 가정하고 추정 해보자.
1. $\arg min_\theta D_{KL}(P||Q_\theta)$
목적식을 전개하면, MLE 목적식과 동일하게 할 수 있다.
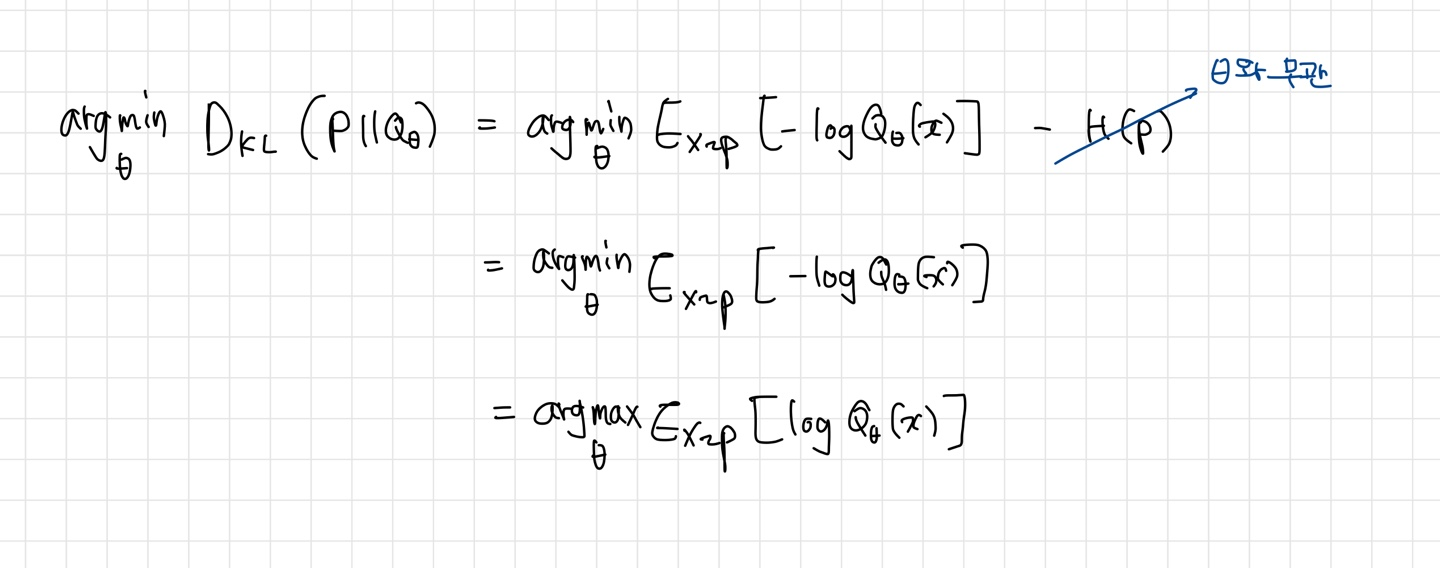
즉, P 분포의 sample point로 Q(x) 확률이 최대가 되는 $\theta$를 찾는 문제다. 따라서 Q(x)는 아래와 같이 정답분포 전 영역에 걸쳐 평균적인 coverage가 좋게 근사하는 분포가 된다. 다시말해, 어떤 정규분포 Q(x)가 정답분포 P(x)를 가장 잘 설명할 수 있을까를 구한 것이다.
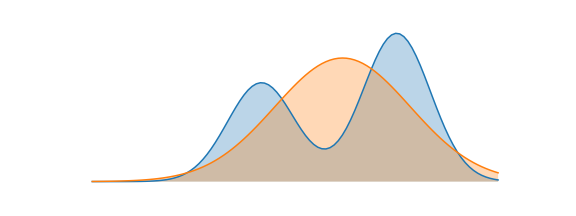
2. $\arg min_\theta D_{KL}(Q_\theta ||P)$
MLE로 해석을 위해 아래와 같이 목적식을 바꿔준다.

최종 목적식은 Q(x)의 sample point에서 P(x) 확률이 최대가 되는 $\theta$를 찾는 문제다. 뒤에 entropy term은 penalize term으로 Q(x)가 가능한 엔트로피가 큰 = 분산이 큰 = 넓게 퍼진 분포를 갖게 한다. 아래와 같이 Q(x)가 추정된다.
$\arg min_\theta D_{KL}(P||Q_\theta)$를 만족하는 Q 분포에 대해 확률을 할당해서 직관과 수식이 동일한지 확인해보자. 계산 편의를 위해 이산확률분포를 가정하고, log0은 -100으로 생각한다.
<1번 - fig.1의 Q 분포>
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Q(X) |
1/8 |
1/8 |
2/8 |
2/8 |
1/8 |
1/8 |
0 |
|
logQ(X) |
-3 |
-3 |
-2 |
-2 |
-3 |
-3 |
-100 |
기댓값은 -15
<2번 - fig.2의 Q 분포>
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Q(X) |
0 |
0 |
0 |
0 |
2/8 |
4/8 |
2/8 |
|
logQ(X) |
-100 |
-100 |
-100 |
-100 |
-2 |
-1 |
-2 |
기댓값은 -53.75
1번 분포의 기댓값이 2번보다 크므로, $\arg min_\theta D_{KL}(P||Q_\theta)$ 경우에 fig.1 처럼 Q 분포가 최적화 되는 것이 자연스럽다. 확률이 0인 점에서 log likelihood가 매우 작은 값을 갖게 되어 기댓값에 dominant한 영향을 준다. 즉 Q 확률이 0에 가까운 점에서는 기댓값의 domain 확률이 작을수록 목적식을 최대화(MLE)한다.
'Statistic' 카테고리의 다른 글
| Hessian 행렬의 고윳값과 definite (0) | 2021.01.15 |
|---|---|
| 독립과 직교(orthogonal) (2) | 2021.01.09 |
| [TIL] Softmax에서 왜 e를 쓸까 (4) | 2020.12.10 |
| [머신러닝] Logistic Regression(MLE와 Bayesian inference를 통한 확률론적 접근) (8) | 2019.11.08 |


