origin paper: https://arxiv.org/pdf/2005.11401.pdf
Overview
문맥 정보를 반영하는 고정된 임배딩 모델 pre-trained neural retriever(Bert)과 seq2seq transformer(Bart)를 결합하여, task specific task에서 더 좋은 성능을 보이는 모델 RAG를 제안
Model

모델은 크게 retriever과 generator로 나뉜다.
retriever

retriever은 우선 큰 데이터 셋(ex. 위키피디아)으로 pre-trained 된 document 임배딩에 대한 인덱스(위 이미지에서 초록색, ex. DOC 46)를 갖고 있다. query encoder를 통해 임배딩 된 인풋과 가까운(내적 기반 코사인 유사도) top-k 개의 doc 임배딩을 찾아 인풋과 doc 임배딩을 concat 한다. 즉 인풋에 doc 문맥 정보를 반영한다.
구체적으로 retriever은 bert 기반의 DPR 모델을 사용한다. query encoder, doc encoder에 서로 다른 pre-trained bert 모델을 사용해 임배딩을 얻는다. 인풋이 x, 위키피디아가 z 일 때, retriever은 다음과 같이 정의된다.
$$retrieval: P_\eta(z|x) = exp(d(z)^Tq(x)) \\ d(z) = bert_d(z), \ q(x) = bert_q(x)$$
가장 높은 확률의 P(z|x)를 찾기 위해 maximum inner product search를 사용한다. 이는 두 임배딩 내적이 커지는 k개의 z를 찾는 알고리즘이고, 결국은 인풋과 가장 유사한 z를 구하게 된다. 학습 시에는 d(z)는 고정시키고 q(x)만 학습시킨다.
이렇게 찾은 z와 x를 concat 해서 generator의 인풋으로 넘긴다.
generator
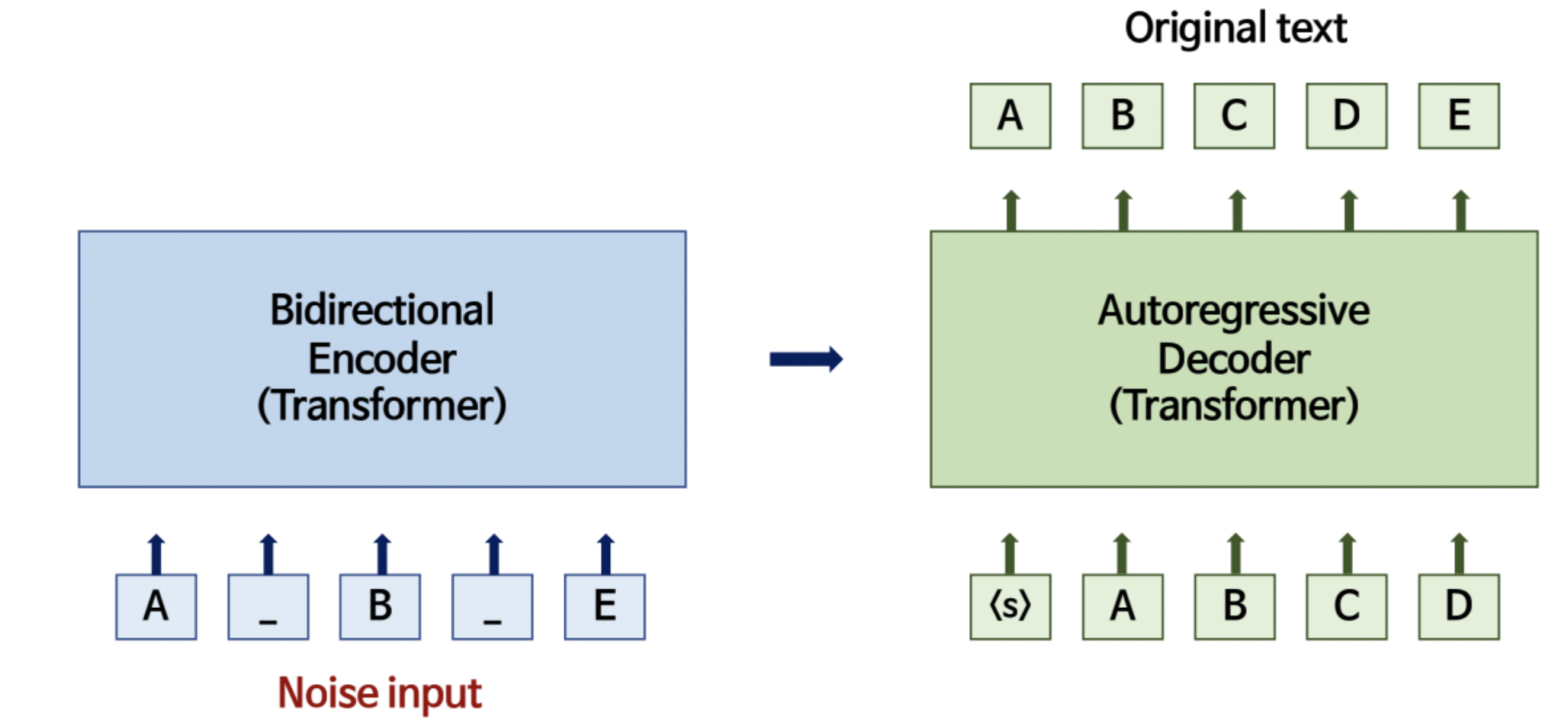
BART 모델 사용, concat 된 x, z와 이전 시점의 target 값, y를 인풋으로 현재 시점의 y를 예측한다. 수식으로 쓰면 다음과 같다.
$$generator: p_\theta(y_i|x,z,y_{i-1})$$
Training
retriever과 generator를 합쳐서 전체 모델을 수식으로 써보면 다음과 같이 k개의 z에 대해 marginalize 한다.
RAG-token: 각 target token을 추정하는데 서로 다른 latent z를 사용
RAG-seqence: z를 maginalize 해서 하나의 latent z로 보고, 이를 사용하여 target sequence 추정
$$P_{RAG-token}(y|x) = \prod_{i}^{N}\sum_{z\in top-k(p(.|x))}p_\eta (z|x)p_\theta(y_i|x,z,y_{1:i-1}) \\ P_{RAG-sequence}(y|x) = \sum_{z\in top-k(p(.|x))}p_\eta (z|x)\prod_{i}^{N}p_\theta(y_i|x,z,y_{1:i-1})$$

이때, 입력 pair $(x_j, y_j)$가 주어지면 Adam을 통해 negative log likelihood, $\Sigma_j -logP(y_j|x_j)$를 최소화한다. 학습 중 doc encoder를 업데이트하면 doc index을 정기적으로 업데이트해야 하므로 비용이 많이 소모된다. 그래서 query encoder와 generator를 fine-tuning 하고 document encoder를 고정상태로 유지한다.
디코딩은 일반적인 beam search를 사용한다.
$$P_{\theta}(y_i|x, y_{1:i-1}) = \sum_{z_i\in top-k(p(.|x))}p_\eta (z_i|x)p_\theta(y_i|x,z_i,y_{1:i-1})$$
Conclusion
기본적인 seq2seq 모델 인풋에 문맥 정보를 반영해서 좀 더 정교하고 특정 domain에 특화된 결과를 얻을 수 있는 모델.
'Paper' 카테고리의 다른 글
| [논문] EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (0) | 2021.05.27 |
|---|---|
| [논문-WIP] Lambda Network(ICLR, 2021) (0) | 2021.04.29 |
| [논문-WIP] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction (0) | 2021.04.15 |
| [논문] BERT4Rec: Sequential Recommendation with BidirectionalEncoder Representations from Transformer (0) | 2021.04.08 |
| [논문] GPT-2 (0) | 2021.03.04 |



