다음의 논문을 공부하며 정리한 글입니다.
https://openreview.net/pdf?id=S1lvm305YQ
INTRODUCTION
음색(Timbre)은 하나의 악기를 다른 악기와 구분하는 인식적 특성(perceptual characteristic)이다. 음색을 모델링하는 것은 매우 어려운 과제다. 한 음에서 음색은 비선형성을 가진다. 전자적으로 음색을 모델링하고 조작할 수 있는 것은 다양한 악기와 음색을 compose하기 원하는 음악가들에게 중요한 역할을 한다. 이 논문에서는 서로 다른 악기로 음색을 변환하는 문제를 다룬다. 구체적으로는 pitch와 loudness와 같은 다른 소리의 특성을 보존하면서 음색을 변환하는 것을 목표로한다. Spectograms을 image-based style transfer에 적용하는 접근을 했지만, spectograms은 위상(phase)정보가 없고, 위상을 추정하기 위한 방법론인 Griffin은 높은 해상력의 오디오 생성에 좋지 않은 characteristic artifacts를 생성하는 문제가 있다.
spectograms은 오디오 데이터 분석에서 기본적인 형태로 phase 정보가 날라간 것은 알고 있었는데, 위와 같은 문제가 있는 줄은 몰랐다. griffin에서 만들어지는 characteristic artifacts 문제를 알고 싶다면, "Natural TTS synthesis by conditioning wavenet on mel spectrogram predictions" 이 논문을 참고하자!
최근 몇년간 audio generation은 빠르게 발전했다. 일례로 Tacotron2는 Mel-spectograms를 이용해 높은 수준의 청각 표현 level에서의 해상력을 올렸다. 연구진은 STFT(short-time fourier transform) 대신 CQT(constant Q transform)를 사용하고 griffin 대신 conditional WaveNet을 이용한 TimbreTron을 제시한다. TimbreTron은 다음의 3-steps으로 이루어져 있다.
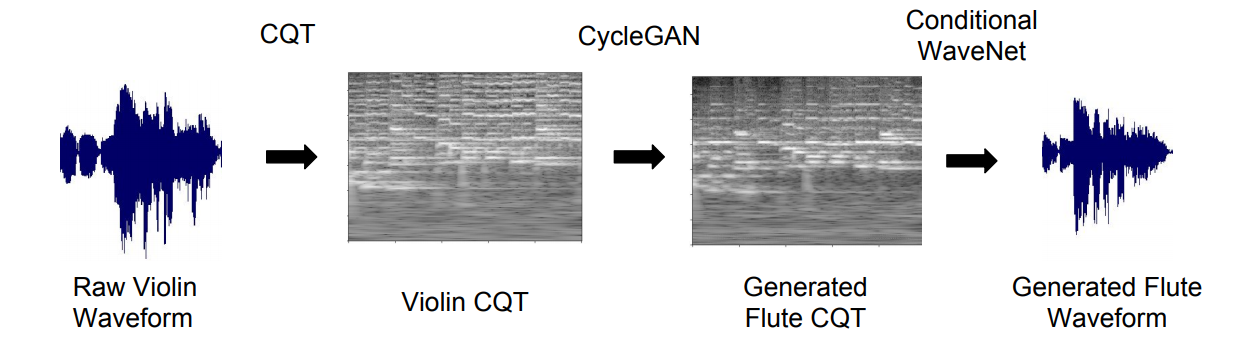
- 악기1의 소리 파형(waveform)에서 CQT Spectogram을 계산해 phase 정보를 버리고 magnitude 값만 이용해 위 두번째 그림과 같은 이미지를 만든다.
- CycleGAN을 사용해 타겟으로 하는 악기2의 CQT Spectograms으로 변환
- 2번에서 생성된 악기2 CQT Spectograms에 WaveNet을 이용해 파형(waveform)으로 복원 : 이 과정에서 phase 정보가 복원되고, 소리를 들을 수 있게된다.
BACKGRAOUD
위상(phase)
반복되는 파형(waveform)의 주기에서 첫 시작점의 위치, 각도로 정의. 따라서 주파수(frequency)와 음압(amplitude)이 같아도 위상이 다르면 다른 음색의 소리가 난다. 푸리에 변환 계수는 주기함수 성분의 amplitude와 phase 정보가 함께 포함되어 있다.

Constant Q Transform(CQT)
STFT와 같은 주파수 분석 방법으로, 서로 다른 주파수 대역들 사이의 기하학적 분해를 고려한다. 위 그림을 보면 CQT는 STFT에 비해 고주파에서 더 많은 정보를 나타내고 있다.
Rainbowgram
CQT phase에 대한 시간 미분 값들을 색으로 나타낸 이미지. 이는 CQT 스펙토그램에서는 보이지 않았던 음색적인 특성을 보여준다. GANSynth에 나왔던 IF, unrapped phase랑 비슷한 개념인듯?

Reconstruction from spectrograms
스펙토그램 단에서 GAN을 이용한 변환을 진행하므로(스펙토그램을 이미지 데이터로 보고) 이를 다시 파형(waveform)으로 바꿔야 소리를 들어볼 수 있다. 파형 복원을 위해선 magnitude와 phase 정보가 모두 필요한데, 앞선 변환에서 phase 정보를 버렸기 때문에 magnitude로 phase를 추정하는 Griffin-Lim 알고리즘을 사용한다. 하지만 introduction에서 살펴 보았듯이, 이 알고리즘의 characteristic artifacts 문제로 이를 WaveNet으로 대체해 복원한다. WaveNet은 해상력을 좋지만 파형을 생성하는데 cost가 많이 든다.
Music processing with constant-q-transform representation
CQT for music representation
CQT로 만든 스펙토그램은 음악 오디오 신호 처리에 적합하다. 주파수의 로그 스케일 표현을 사용하는데 이는 12음계의 피치를 커버하는데 적합하다. STFT에 비해 낮은 주파수 대역에서는 높은 주파수 해상도를 갖고, 높은 주파수 대역에서는 더 높은 시간 해상도를 갖는다. 이는 첼로와 트롬본 같은 주파수 대역이 낮은 악기의 해상력과 리듬의 미세한 시간 정보 복원에 이점이 있다.
또한 CQT는 pitch equivanriance라는 중요한 특성을 가진다.
Thanks to the geometric spacing of frequencies, a pitch shift corresponds (approximately) to a vertical translation of the “spectral signature” (unique pattern of harmonics) of musical instruments. This means that the convolution operation is approximately equivariant under pitch translation, which allows convolutional architectures to share structure between different pitches. A demonstration of this can be seen in Figure 3. Since the harmonics of a musical instrument are approximately integer multiples of the fundamental frequency, scaling the fundamental frequency (hence the pitch) corresponds to a constant shift in all of the harmonics in log scale.
WAVEFORM RECONSTRUCTION FROM CQT REPRESENTATION USING CONDITIONAL WAVENET
40개 layer를 가진 조건부 WaveNet을 사용하고 인풋 데이터는 CQT와 파형(waveform)을 쌍으로 훈련시켰다. WaveNet을 오디오 샘플 특성에 맞춰 재구축했다. Beam search와 Reverse generation 방법을 통해 훈련했다. 전자는 타겟 CQT를 더 잘 fitting 시키기 위함이고, 후자는 타악기와 같이 갑자기 음이 튀었다가 점점 낮아지는 것을 모델링 하기위해 거꾸로 뒷부분 부터 생성하는 방법이다.
TIMBRE TRANSFER WITH CYCLEGAN ON CQT
결국, TimbreTron 모델은 log-amplitude CQT를 하나의 이미지로 보고 image-to-image로 변환/학습시키는 것이다. 이를 위해 CycleGAN을 사용한다. 그대로 쓰지는 않고 소리에 대한 시간-주파수 표현에 적합하게 다음과 같은 fine-tuning을 해준다.
'Paper' 카테고리의 다른 글
| [논문] Symbolic Music Genre Transfer with CycleGAN (ETH Zurich, 2018) (0) | 2020.03.23 |
|---|---|
| [논문] Lexicon-Free Conversational Speech Recognition with Neural Networks (0) | 2020.03.18 |
| [논문] CAM, Grad-CAM (0) | 2019.12.03 |
| [논문] YOLO (0) | 2019.11.19 |
| [논문]ResNet (0) | 2019.11.14 |

